Euclide

Euclide, effectuant probablement une construction géométrique au compas, vu par le peintre Juste de Gand.

Euclide est un mathématicien grec qui aurait vécu entre les IV^e et III^e siècles av. J-C Il est connu pour ses écrits, notamment les Éléments, sur lesquels repose une grande partie des mathématiques.

Biographie

Euclide est un mathématicien grec considéré comme le père de la géométrie. Il est présumé né à Athènes vers -330 . Il étudia tout d'abord à « l'école des successeurs de Platon » dans sa ville natale. Puis il fut invité par Ptolémée I^er à la grande « école d'Alexandrie » en Égypte. Il y dirigea une équipe de mathématiciens. Il serait mort à 65 ans dans la ville d' Alexandrie (Égypte) vers 265 avant J.-C.il a inventé les divisions euclidiennes.

• Le domaine de recherche principal d'Euclide était la géométrie. Il écrivit une encyclopédie composée de 13 livres, « Les éléments », ce sera la base de la géométrie pendant plus de 2 000 ans. C'est l'ouvrage le plus édité après la Bible.

• Euclide s'intéressait aussi à l'arithmétique. Il invente un algorithme célèbre qui porte le nom d'algorithme d'Euclide, permettant de calculer le PGCD (plus grand diviseur commun) de deux nombres.

• Il a apporté à la science de l'antiquité, une œuvre qui rassemble toutes les connaissances de son époque auxquelles il a ajouté son savoir. Il a aussi permis à des savants de grandes découvertes. Plus tard Archimède de Syracuse profitera de son travail pour découvrir la quadrature du cylindre.

Les éléments

Page de titre de la première édition anglaise des Éléments.

Les Éléments sont un ensemble de treize livres. À ces treize livres s'ajoutent deux autres dit apocryphes, c'est-à-dire qu’on n'est pas sûr que l’auteur soit bien Euclide : le livre XIV, rédigé par Hypsiclès (astronome et mathématicien grec, II^e siècle apr. J-C), et le livre XV (VI^e siècle) qui traitent tous deux des polyèdres réguliers.

La méthode axiomatique

Dans les Éléments, Euclide applique pour la première fois la méthode axiomatique : il pose cinq affirmations, les axiomes (ou postulats), et construit sa théorie, la géométrie euclidienne, par déductions à partir de ces axiomes.

1. Entre deux points quelconques, il existe une droite.
2. Un segment peut être prolongé en une droite.
3. Avec un segment quelconque, on peut tracer un cercle en prenant ce segment comme son rayon et l’une de ses extrémités comme son centre.
4. Tous les angles droits sont égaux entre eux.
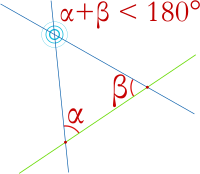
5. Si deux droites coupent une même troisième en produisant, du même côté, des angles dont la somme est inférieure à deux angles droits, alors ces deux droites se coupent entre elles de ce côté de la troisième.

Illustration du 5^e postulat : les deux droites bleues coupent la verte avec des angles α et β dont la somme (α+β) est inférieure à deux angles droits (2×90° = 180°). On constate que les deux droites bleues se coupent bien du même côté que ces angles.

Ils nous semblent évidents (d’où leur nom, du grec ancien αξιωμα/axioma, « considéré comme digne, convenable, évident en soi »), mais étaient impossibles à démontrer et devaient donc être acceptés sans démonstration pour permettre de travailler sur la géométrie.

Le cinquième axiome, souvent appelé « postulat d’Euclide », a longtemps été considéré comme superflu : on a pensé qu’il était plutôt un théorème que l’on pouvait démontrer en utilisant les quatre autres axiomes. Aujourd'hui, la communauté scientifique considère qu’il est bien un axiome, c’est-à-dire qu’il ne se démontre pas.

On peut construire d’autres géométries, appelées géométries non euclidiennes, en changeant juste ce cinquième postulat mais, à l’époque d’Euclide, ces géométries alternatives n’étaient pas connues.

Contenu

Les livres I à IV concernent la géométrie du plan ; les livres V et VI traitent des proportions ; les livres VII, VIII et IX réunissent des travaux d’arithmétique ; à partir du livre XI et jusqu'au XV, il est question de géométrie dans l’espace. Les livres V et X sont les plus subtils.

1. Le premier livre des Éléments commence par définir la notion de point, de ligne (droite) et de segment, puis présente les cinq postulats (« demandes ») et les « notions ordinaires » . Il traite ensuite notamment de la construction du triangle équilatéral, de la somme de ses angles et du théorème de Pythagore (dont il effectue la toute première démonstration).
2. Le second livre s’occupe des bases de l’algèbre géométrique, c’est-à-dire des relations entre les nombres considérés géométriquement (longueur de segments, aires). Euclide y démontre ainsi, entre autres, les identités remarquables courantes et y évoque un cas particulier d’une équation du second degré.
   

   Le cercle inscrit à un triangle
3. Le livre III traite des propriétés du cercle et des tangentes.
4. Le livre IV étudie la construction des polygones, ainsi que leur inscription  et circonscription  par le cercle.
5. Le livre V, consacré à la notion de rapport (proportion entre deux grandeurs), est parfois attribué au pythagoricien  Eudoxe. Il reprend en effet les travaux des pythagoriciens concernant les proportions, mais les étend aux nombres dits « incommensurables » (on parle aujourd'hui de nombres irrationnels, comme √2). Ce livre, précurseur et très tardivement compris, servira de base aux travaux de Karl Weierstrass puis de Richard Dedekind, mathématiciens allemands du XIX^e siècle.
6. Le livre VI applique la théorie des proportions présentée au livre V pour étudier les similitudes dans le plan et démontrer le théorème de Thalès.
7. Le livre VII (comme les deux suivants) est consacré à la théorie des nombres (l’arithmétique). Il traite de la divisibilité des nombres entiers et, par conséquent, des notions de nombre premier, PGCD et PPCM. On y trouve pour la première fois l’algorithme d'Euclide.
8. Le livre VIII étudie les suites géométriques et encore les proportions.
9. Le livre IX démontre, par l’absurde, qu’il existe une infinité de nombres premiers. Il propose également une ébauche de démonstration du théorème fondamental de l'arithmétique : «Tout nombre entier se décompose de manière unique en un produit de nombres premiers.» et donne le résultat de la somme d’une suite géométrique. Il aborde enfin la notion de nombre parfait.
   

   Le tétraèdre (4 faces)
10. Le livre X, très long et difficile, démontre que √2 est un nombre irrationnel et tente de classer les « lignes commensurables » et « incommensurables » (nombres rationnels et irrationnels) entre elles en fonction de leur longueur.
11. Le livre XI commence l’étude des solides  en généralisant les propriétés des figures du plan (vues aux livres I à VI) à l’espace.
12. Le livre XII présente la méthode dite « d’exhaustion » (sorte d’intégration, reprise plus tard par Archimède) et l’applique au calcul des aires et volumes de solides usuels : pyramides, cylindres, sphère, etc. Comme le livre V, il est parfois attribué à Eudoxe.
13. Le livre XIII, enfin, traite la construction à la règle et au compas des cinq polyèdres réguliers de Platon : tétraèdre (4 faces), cube (6 faces, aussi appelé hexaèdre), octaèdre (8 faces), dodécaèdre (12 faces) et icosaèdre (20 faces), en utilisant les résultats du livre X et généralise l’usage du nombre d'or à l’espace (« section dorée »).

Notes

Le peu que l’on sait d’Euclide nous vient des écrits d’autres auteurs.

• Proclos, un philosophe athénien du V^e siècle apr. J-C : Euclide aurait étudié à Athènes puis serait parti, à l’invitation du pharaon Ptolémée I^er, enseigner à Alexandrie.
• Apollonios de Perga, géomètre et astronome grec : il aurait passé beaucoup de temps avec les disciples d’Euclide ; il en parle dans un ouvrage paru entre la fin du III^e siècle av. J-C et le début du II^e siècle av. J-C.
• Les mathématiques qu’expose Euclide sont plus avancées que celles de Platon et Aristote et reprennent des travaux d’Eudoxe, ce qui impliquerait qu’il ait vécu après eux, c’est-à-dire soit à la fin du IV^e siècle av. J-C, soit au III^e siècle av. J-C.

Certains travaux qui lui sont attribués auraient été écrits par ses disciples, ce qui expliquerait des problèmes de chronologie et les différents styles de rédaction entre les treize tomes des Éléments.

Son nom a longtemps été confondu avec celui du philosophe grec Euclide de Mégare (environ IV^e siècle av. J-C) par ses traducteurs au Moyen Âge et à la Renaissance, comme le montre l’illustration précédente (au bas de laquelle on peut lire Euclidi Megaren).

Sources

• Encyclopédie Universelle
• Wikipédia

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...