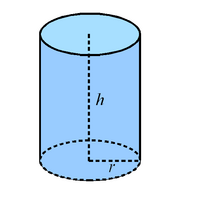
Cylindre

Cet article est une ébauche. Améliore le !

Cylindre de révolution, de hauteur h et de rayon r.

En géométrie, un cylindre est un solide, c'est-à-dire un objet de l'espace (qui occupe donc un certain volume). Il existe deux façons de « construire » un cylindre :

• la plus commune consiste à faire tourner un parallélogramme autour d'un axe (une droite), dit axe de révolution, un peu comme une porte pivote sur ses gonds : le côté du parallélogramme « attaché » à l'axe ne bouge pas, et la surface cylindrique est « dessinée » (on dit décrite) par le côté opposé. Pour un tour complet du parallélogramme autour de l'axe, tous les points de l'espace qui ont « touché » ce côté (sur la porte, le côté de la poignée) forment la surface cylindrique.
• on peut aussi voir un cylindre comme un empilement de cercles les uns sur les autres ; mais cela n'a pas vraiment de réalité mathématique.

Une fois la surface cylindrique décrite, on « ferme » le cylindre par ses bases : celles-ci correspondent par exemple aux extrémités d'un sablier, sur lesquelles on pose l'objet (parce que sinon, le cylindre roule !). On appelle hauteur du cylindre la distance qui sépare les deux bases.

Parmi les cylindres, on distingue le cylindre dit « de révolution » : c'est un cylindre dont les parois (les « côtés ») sont parallèles à l'axe de révolution.

Les cylindres ne sont pas que des figures abstraites. On les rencontre dans la vie de tous les jours : des rondins de bois aux colonnes des temples, des craies aux tours circulaires, etc. L'homme a su exploiter l'avantage des cylindres de révolution, notamment en architecture !

Description, géométrie

Un cylindre présente deux bases. Bien qu'on appelle généralement « cylindre » seulement les cylindres de révolution, dont les bases sont des cercles, les cylindres au sens large peuvent avoir comme bases deux disques, deux carrés, deux rectangles, deux losanges, etc., toujours identiques et parallèles. Ainsi, un cube est un cas particulier du cylindre !

La seconde base s'obtient à partir de la première en effectuant une translation dans l'espace. Cette translation va « décrire du volume » : c'est le cylindre.

Les bases ont la même forme et les mêmes dimensions : elles ont en particulier la même aire. Les bases sont inscrites dans deux plans parallèles, séparés par une distance appelée la hauteur du cylindre.

Le volume du cylindre est le produit de l'aire de la base par la hauteur.

Par exemple, si la base fait 40m² et la hauteur 10m, alors le volume fait 400 m³.
À ce propos, il s'agit de bien remarquer que si une longueur s'exprime en mètres, un volume se donne en mètres cube (et une surface en mètres carré).

La translation s'effectue selon une direction qui peut être plus ou moins inclinée par rapport au plan de départ (la première base). Lorsque le déplacement s'effectue dans une direction orthogonale à ce plan (perpendiculaire à ce plan), on parle de cylindre droit. Le cylindre de révolution en est un cas particulier.

Cylindre de révolution

Le cylindre de révolution se présente comme :

• un disque de centre O et de rayon R décrit dans un plan P ;
• une droite D orthogonale à P ; cette droite passe par O et un point A, tel que la distance AO sera la hauteur du cylindre ;
• un seconde disque, identique au premier mais de centre A, décrit dans le plan parallèle à P passant par A.

Pourquoi cylindre de révolution ? En sciences, la révolution est un mouvement de rotation (par exemple : la révolution de la Terre autour du Soleil). Le cylindre de révolution peut être obtenu en partant d'un rectangle dont les côtés ont pour longueur R (le rayon du disque évoqué plus haut) et AO et en faisant une rotation autour de l'une de ses médiatrices.

Le volume d'un cylindre est donné par la formule :

π × R² × h

où R est le rayon du cercle formant la base, et h la hauteur du cylindre.

Dans la vie de tous les jours

Rondins de bois, benne, boîtes de conserve, rouleaux de papier adhésif et craies ont une forme de cylindre.

De nombreux objets autour de nous ont la forme d'un cylindre. Souvent, ce sont des objets fabriqués par l'homme, et la forme est recherchée et voulue.
En voici quelques exemples :

• Quand le bûcheron coupe le tronc d'un arbre, il forme des rondins de bois. On peut en rencontrer en se promenant en forêt. Si l'on a une cheminée pour se chauffer l'hiver, alors on y fait brûler des rondins de bois (et des brindilles), qui s'achètent souvent par stères.
• Certaines bennes de camion ont la forme d'un cylindre. Ces camions transportent des liquides (carburant, lait, vin, produits chimiques liquides...), on les appelle camions-citernes.
• Les boîtes de conserve ont aussi la forme d'un cylindre. Elles servent par exemple à conserver des légumes. Ces boîtes de conserve sont faciles à produire en série, et peuvent avoir différentes formes, selon les marques et le contenu.
• Les rouleaux de papier adhésif prennent la forme d'un cylindre. Ils sont faciles à dérouler, et contiennent souvent une grande quantité de papier adhésif occupant une petite place.
• Les craies qu'utilise l'instituteur ou le professeur au tableau ont la forme d'un cylindre. Les stylos en ont une forme très proche. Petits, ils sont très faciles à tenir et manipuler.

Exemple d'un minaret.

Les cylindres sont aussi utilisés en architecture. Le premier élément de l'architecture est les colonnes, qui soutiennent les plafonds, ou les voûtes. Les colonnes étaient déjà utilisées par les premières civilisations. Elles ont une forme cylindrique, car un cylindre peut facilement s'obtenir en empilant les pierres les unes par-dessus les autres. En Égypte antique, en Grèce antique et dans la Rome antique, les colonnes dans les palais ou les temples ont la forme d'un cylindre de révolution. Elles sont utiles, mais constituent aussi un élément de décoration.

Bâtiments aux fonctions multiples, les tours peuvent aussi avoir une forme en cylindre. Par exemple, dans les mosquées, le minaret une tour au sommet de laquelle l'imam appelait les fidèles à la prière. En général, le minaret a la forme d'un cylindre de révolution, mais peut aussi avoir une base carrée, par exemple au Maroc. La forme des minarets varie d'un pays à l'autre.
Il faut noter que, dans le cas des tours, la forme cylindrique n'a pas qu'un rôle esthétique : la force du vent est moins importante sur un cylindre de révolution que par exemple sur un cube (car il y a moins de surface face au vent), et l'on peut donc construire des tours plus hautes et moins fragiles.

Portail des mathématiques - Les nombres, la géométrie et les grands mathématiciens.