Identité remarquable

En mathématiques, une identité remarquable est une égalité vérifiée par tous les nombres et qui permet d'accélérer les calculs. Certaines servent à développer des produits, à factoriser des sommes ou à simplifier des expressions.

Pour les utiliser efficacement, il est nécessaire de les connaître par cœur, ou du moins de les retenir sous forme de règles.

Donnons les plus importantes :

• trinôme carré parfait : (a + b)² = a² + 2ab + b² ;

• trinôme carré parfait : (a – b)² = a² - 2ab + b² ;

• différence de carrés : (a – b)(a + b) = a² – b² ;

• (a + b)³ = a³ + 3a²b + 3ab² + b³.

		Le savais-tu ?
	Preuve géométrique !
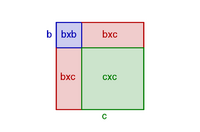
Certaines identités peuvent se démontrer facilement par des constructions géométriques relativement simples. En voici un exemple avec le trinôme carré parfait : Soit un carré de côté de longueur a + b. On peut le diviser en un carré de côté de longueur a, en un autre carré de côté de longueur b et en deux rectangles de côtés de longueurs a et b. Par conséquent, (a + b)² = a² + 2ab + b².

Factorisation de polynômes

Cet article semble trop confus et / ou trop compliqué. N’hésitez pas à le simplifier ou à donner votre avis. Aide sur la syntaxe wiki – Conseils de rédaction

Article à créer : polynôme

Comment factoriser le polynôme X⁴ + a⁴ ?

Comme le polynôme X⁴ + a⁴ prend des valeurs strictement positives sur tout nombre réel, il n'admet aucune racine réelle. Le polynôme va donc se factoriser en un produit de deux polynômes réels de degré 2. La question est de savoir lesquels.

• Première étape : par application du binôme de Newton, on obtient :
•  : X⁴+a⁴=X⁴+2a²X²+a⁴-2a²X²=(X²+a²)²-(sgrt (2) aX)² ;
• Seconde étape : on applique la différence de carrés :
•  : (X²+a²)²-(sqrt (2) aX)²=(X²-sqrt (2) aX+a²) (X²+sqrt (2) aX+a²).

Pour résumer, on a obtenu la factorisation :

X⁴+a⁴=(X²-sqrt (2) aX+a²) (X²+sqrt (2) aX+a²)

		Le savais-tu ?
	L'erreur de Leibniz
En 1702, le mathématicien Leibniz affirma que le polynôme X4+a4 ne pourrait pas se factoriser. À l'époque, la formule du binôme de Newton était connue, mais il n'a pas pensé à l'appliquer ! Son raisonnement, évidemment faux, était basé sur une mauvaise compréhension de la nature des nombres complexes appelés quantités imaginaires. Les nombres réels étaient connus, et les gens supposaient l'existence des racine des polynômes sans trop se poser de questions sur la nature des racines. Leibniz essaya de calculer les racines de X4+a4, et la formule qu'il a obtenue lui fit croire à tort que ces racines ne seraient pas complexes (elles le sont évidemment !). Il conclut que le polynôme X4+a4 ne pourrait pas être factorisé en produit de deux polynômes de degré 2. On vient d'obtenir le contraire... Tous les polynômes à coefficients réels peuvent se factoriser en produit de polynômes de degré 1 ou 2. Mais ce théorème énoncé fut énoncé pour la première fois par Euler en 1742. D'autres après Leibniz commirent des erreurs semblables.