Fonction exponentielle

Chaque cellule se sépare régulièrement en deux cellules identiques : leur nombre augmente de façon exponentielle.

Graphe de la fonction exponentielle

En mathématiques, parmi toutes les fonctions, il en existe une importante : la fonction exponentielle. Elle représente souvent quelque chose qui augmente de plus en plus vite. Sur un graphe, elle a une courbe reconnaissable, très plate à gauche puis grimpant en pente vertigineuse à droite.

Utilisations courantes

Dans la nature, en informatique ou dans la société, on dit de nombreux phénomènes qu'ils suivent « une loi exponentielle ». Cela signifie que leur évolution dans le temps ressemble à une fonction exponentielle : ces phénomènes augmentent de plus en plus vite, comme une multiplication à chaque instant. Ce n'est pas comme une augmentation régulière (« linéaire ») ou on ajoute le même nombre à chaque instant.

On parle de loi exponentielle pour :

• le développement de populations, en particulier de certaines bactéries ;
• le phénomène de radioactivité ;
• le temps d'exécution des moins bons algorithmes en informatique ;
• la libération d'énergie dans une bombe nucléaire ;
• la diffusion d'informations sur Internet, et principalement sur les grands réseaux sociaux comme Facebook ;
• la propagation d'épidémies devenant ensuite pandémies ;
• etc.

Tous ces phénomènes sont caractérisés comme étant un peu « lents » à démarrer, pour ensuite connaître une évolution dans le temps de plus en plus rapide et importante.

• 

  La puissance des ordinateurs double tous les 5 ans (loi de Moore). C'est bien une loi exponentielle : ici, la courbe est droite, ce sont les graduations verticales qui augmentent de façon exponentielle — ce qui revient au même.

• 

  La courbe d'estimation du nombre de cas à l'épidémie de Covid-19 à Wuhan suit une croissance exponentielle.

Exemple

Si quelqu'un a deux chevaux au départ et qu'il en veut un de plus chaque année, il en aura 2 puis 3 puis 4 puis 5... et 10 au bout de 8 ans, 22 au bout de 20 ans. L'augmentation du nombre de ses chevaux dans le temps est alors une fonction affine : il suffit d'ajouter 2 au nombre d'années pour avoir le nombre de chevaux.

Cependant, les chevaux se reproduisent. Disons que chaque couple de chevaux a deux petits tous les 4 ans, et que les chevaux ne meurent jamais. À partir de deux chevaux, sans en acheter ni en vendre, leur nombre est multiplié par 2 tous les 4 ans : il en aura :

• 2 × 2 = 2² = 4 après 4 ans,
• 2 × 2 × 2 = 2³ = 8 après 8 ans,
• 2 × 2 × 2 × 2 = 2⁴ = 16 après 12 ans,
• 2 × 2 × 2 × 2 × 2 = 2⁵ = 32 après 16 ans,
• 2 × 2 × 2 × 2 × 2 × 2 = 2⁶ = 64 après 20 ans…

Dans ce cas, c'est une fonction exponentielle. Elle peut augmenter moins vite qu'une fonction affine au début, mais bientôt elle augmente beaucoup plus vite.

Propriétés mathématiques

La fonction exponentielle s'écrit le plus souvent exp ou $x\mapsto e^{x}$ et possède certaines particularités :

• elle n’est jamais nulle, c'est-à-dire que son résultat n'est jamais 0 : même si on dirait qu'elle se confond, vers la gauche du graphe, avec l'axe (horizontal) des abscisses, elle ne l'atteint en fait jamais (on appelle cela une asymptote) ;
• elle est strictement croissante sur l'intervalle des nombres réels : elle ne « diminue » jamais en allant vers la droite du graphe et ne fait même jamais de « pause » ;
  

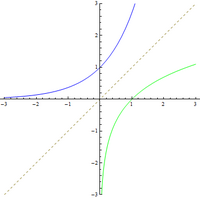  En bleu : la fonction exponentielle ; en vert : la fonction logarithme ; en pointillés gris : la première bissectrice (qui associe à chaque nombre lui-même). La fonction exponentielle de base e est la réciproque du logarithme de base e
• elle est elle-même sa propre fonction dérivée ;
• c'est une fonction qui « croît » plus rapidement que n'importe quelle fonction polynômiale ;
• les fonctions sinus et cosinus s'expriment avec la fonction exponentielle (dans sa version complexe) : $\exp(\mathrm {i} x)=\cos(x)+\mathrm {i} \sin(x),$;
• c'est la bijection réciproque de la fonction logarithme népérien ;
• c'est grâce à elle que sont définies les fonctions puissance.

Typiquement, on peut définir la fonction exponentielle de deux manières :

1. soit comme la seule fonction qui, à la fois :
   • est sa propre dérivée ;
   • vérifie l'égalité e⁰ = 1 (on dit que c'est la seule solution de la plus simple équation différentielle : g’ = g avec la condition g(0) = 1). e est appelé le nombre d'Euler et vaut 2,718.
2. soit, indirectement, en disant que c'est la réciproque de la fonction logarithme népérien ; cela revient à définir l'exponentielle comme la fonction dont la courbe est le symétrique de celle de la fonction logarithme par rapport à la première bissectrice .

La fonction exponentielle possède quelques propriétés calculatoires :

• Relation fonctionnelle : $\exp {(a)}\exp {(b)}=\exp(a+b)$
• $\exp(-x)={\frac {1}{\exp(x)}}$
• $\forall n\in \mathbb {Z} ,\exp(x)^{n}=\exp(nx)$
• $\exp(x-y)={\frac {\exp(x)}{\exp(y)}}$

Fonction exponentielle de base a

Graphe de la fonction exponentielle de base a

La fonction exponentielle de base a est une généralisation de la fonction exponentielle. Elle se note : $x\mapsto a^{x}$. En plus des propriétés calculatoires de la fonction exponentielle, elle admet aussi cette propriété supplémentaire : $a^{x}=\exp(x\ln(a))={\rm {e}}^{x\ln(a)}$

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...