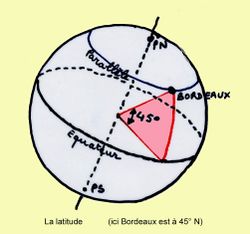
Parallèle (géographie)
Un parallèle est un cercle imaginaire dont le tracé est parallèle à celui de l'équateur terrestre. C'est aussi l'intersection avec la surface de la Terre d'un plan imaginaire parallèle au plan équatorial. Le parallèle a pour seul but de donner la latitude d'un point de la surface terrestre.
On a créé 90 parallèles dans l'hémisphère Nord et autant dans l'hémisphère Sud. Chaque parallèle correspond à un angle de latitude mesuré depuis l'équateur et exprimé en degrés. Entre deux parallèles successifs on peut en créer d'autres pour tenir compte des valeurs d'angle inférieures au degré (les minutes et les secondes d'angle).
Propriétés[modifier | modifier le wikicode]
Les cercles parallèles sont des loxodromies (chaque parallèle coupe tous les méridiens sous un même angle) ; ils ne sont donc pas porteurs de directions (seules les orthodromies le sont) à l'exception de l'équateur. En effet, celui-ci est un grand cercle aussi bien sur l'ellipsoïde que sur la sphère. Il ne peut toutefois être une orthodromie (le chemin le plus court) qu'en cas de modélisation sur la sphère. Les parallèles autres que l'équateur n'indiquent donc ni l'est ni l'ouest d'un point quelconque situé sur le globe. À l'inverse, n'importe quel méridien est orienté nord-sud.
En cas de projection cylindrique, et uniquement dans ce cas (projections de Mercator ou de Gall-Peters), tous les parallèles sont perpendiculaires à tous les méridiens.
Le parallèle et son rayon[modifier | modifier le wikicode]
Le rayon d'un parallèle est toujours perpendiculaire à l'axe de rotation terrestre. La longueur du rayon d'un parallèle diminue d'autant plus que la latitude se rapproche des régions polaires. Cette dimension est nulle aux pôles, égale au demi-grand axe de l'ellipsoïde à l'équateur (rayon équatorial en projection sphérique). À l'inverse, la courbure de chaque cercle de latitude augmente lorsqu'on se dirige vers les régions polaires tandis que l'angle d'intersection entre le plan parallèle et le plan tangent à la sphère (au point considéré) diminue : il est de 90° à l'équateur et devient nul aux pôles. La circonférence équatoriale est donc perpendiculaire aux méridiens qui la coupent.
Quant à l'intersection entre les méridiens et les parallèles autres que l'équateur, il n'y a pas lieu de s'en préoccuper ici. Tout simplement parce que les angles sphériques ne sont définis que par les arcs de grands cercles. D'autre part, seul le rayon sphérique est perpendiculaire au plan tangent à la surface. À l'exception de l'équateur, les parallèles sont des petits cercles et ne sont pas des géodésiques. Il n'est donc pas sensé de parler d'angles impliquant les parallèles. Pour information, les méridiens et les grands cercles est-ouest (du point d'intersection) se croisent à angles droits.
|
