Communauté • Livre d'or
Actualités, astuces, interview... Venez lire la gazette de ce printemps de Vikidia ! 
Actualités, astuces, interview... Venez lire la gazette de ce printemps de Vikidia ! 
« Fonction exponentielle » : différence entre les versions
Aller à la navigation
Aller à la recherche
m (Lien interwiki) |
m (Typographie) |
||
| Ligne 21 : | Ligne 21 : | ||
*elle est strictement croissante sur l'intervalle des [[nombre réel|nombres réels]] ; [[Image:Exponentielle et logarithme.png|thumb|En bleu : la fonction exponentielle ; en vert : la [[fonction logarithme]] ; en pointillés gris : la première bissectrice.]] | *elle est strictement croissante sur l'intervalle des [[nombre réel|nombres réels]] ; [[Image:Exponentielle et logarithme.png|thumb|En bleu : la fonction exponentielle ; en vert : la [[fonction logarithme]] ; en pointillés gris : la première bissectrice.]] | ||
*elle est elle-même sa propre [[fonction dérivée]] ; | *elle est elle-même sa propre [[fonction dérivée]] ; | ||
*c'est une fonction qui « croît » plus rapidement que n'importe quel [[polynôme]]; | *c'est une fonction qui « croît » plus rapidement que n'importe quel [[polynôme]] ; | ||
*les fonctions [[sinus]] et [[cosinus]] découlent de la fonction exponentielle (dans sa version [[nombre complexe|complexe]]) ; | *les fonctions [[sinus]] et [[cosinus]] découlent de la fonction exponentielle (dans sa version [[nombre complexe|complexe]]) ; | ||
*c'est la [[bijection]] [[fonction réciproque|réciproque]] de la [[fonction logarithme népérien]] ; | *c'est la [[bijection]] [[fonction réciproque|réciproque]] de la [[fonction logarithme népérien]] ; | ||
*c'est grâce à elle que sont définies les [[fonction puissance|fonctions puissance]] ; | *c'est grâce à elle que sont définies les [[fonction puissance|fonctions puissance]] ; | ||
*et de nombreuses autres choses, mais plus compliquées ... | *et de nombreuses autres choses, mais plus compliquées... | ||
Typiquement, on peut définir la fonction exponentielle de deux manières : | Typiquement, on peut définir la fonction exponentielle de deux manières : | ||
| Ligne 31 : | Ligne 31 : | ||
:#est sa propre dérivée | :#est sa propre dérivée | ||
:#vérifie l'égalité <math>\exp 0 = 1~</math> | :#vérifie l'égalité <math>\exp 0 = 1~</math> | ||
:#:(on dit que c'est la seule solution de la plus simple [[équation différentielle]] : <math>y' = y</math>, avec comme condition : y(0) = 1) | :# : (on dit que c'est la seule solution de la plus simple [[équation différentielle]] : <math>y' = y</math>, avec comme condition : y (0) = 1) | ||
*ou indirectement, en disant que c'est la [[fonction réciproque|réciproque]] de la fonction logarithme népérien ; | *ou indirectement, en disant que c'est la [[fonction réciproque|réciproque]] de la fonction logarithme népérien ; | ||
*:cela revient à définir l'exponentielle comme la fonction dont la courbe est le [[symétrie|symétrique]] de celle de la [[fonction logarithme]] par rapport à la première bissectrice<ref>La '''première bissectrice''' est la droite d'équation <math>y = x</math>. C'est aussi la courbe de la [[fonction identité]].</ref>. | * : cela revient à définir l'exponentielle comme la fonction dont la courbe est le [[symétrie|symétrique]] de celle de la [[fonction logarithme]] par rapport à la première bissectrice<ref>La '''première bissectrice''' est la droite d'équation <math>y = x</math>. C'est aussi la courbe de la [[fonction identité]].</ref>. | ||
==Références== | ==Références== | ||
Version du 17 février 2010 à 11:20
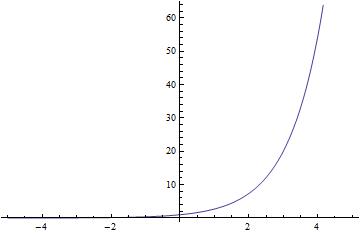
En mathématiques, parmi toutes les fonctions, il en existe une très importante : la fonction exponentielle. On commence à l'étudier en classe de terminale scientifique.
Utilisations courantes
Dans la nature, en informatique ou dans la société, on dit de nombreux phénomènes qu'ils suivent « une loi exponentielle ». Cela signifie que leur évolution dans le temps peut être prédite grâce à la fonction exponentielle.
On parle ainsi de loi exponentielle pour :
- le développement de populations, en particulier de certaines bactéries
- le phénomène de radioactivité
- le temps d'exécution des moins bons algorithmes en informatique
- la libération d'énergie dans une bombe nucléaire
- la diffusion d'informations sur Internet, et principalement sur les grands réseaux sociaux comme Facebook
- la propagation d'épidémies
- etc.
Tous ces phénomènes sont caractérisés comme étant un peu « lents » à démarrer, pour ensuite connaître une évolution dans le temps de plus en plus accélérée et importante.
Généralités
Elle s'écrit couramment ou , et possède certaines particularités :
- elle est strictement croissante sur l'intervalle des nombres réels ;
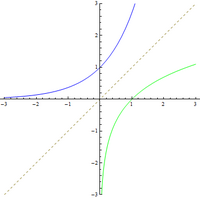En bleu : la fonction exponentielle ; en vert : la fonction logarithme ; en pointillés gris : la première bissectrice. - elle est elle-même sa propre fonction dérivée ;
- c'est une fonction qui « croît » plus rapidement que n'importe quel polynôme ;
- les fonctions sinus et cosinus découlent de la fonction exponentielle (dans sa version complexe) ;
- c'est la bijection réciproque de la fonction logarithme népérien ;
- c'est grâce à elle que sont définies les fonctions puissance ;
- et de nombreuses autres choses, mais plus compliquées...
Typiquement, on peut définir la fonction exponentielle de deux manières :
- comme la seule fonction qui :
- est sa propre dérivée
- vérifie l'égalité
- : (on dit que c'est la seule solution de la plus simple équation différentielle : , avec comme condition : y (0) = 1)
- ou indirectement, en disant que c'est la réciproque de la fonction logarithme népérien ;
- : cela revient à définir l'exponentielle comme la fonction dont la courbe est le symétrique de celle de la fonction logarithme par rapport à la première bissectrice1.
Références
- ↑ La première bissectrice est la droite d'équation . C'est aussi la courbe de la fonction identité.
|
Portail des mathématiques — Les nombres, la géométrie, les grands mathématiciens... |