Graphe (théorie des graphes)

Un graphe : des sommets (ronds et noirs) reliés par des arêtes.

Un graphe est un objet composé de sommets (ou nœuds) et d’arêtes (ou arcs, dans certains cas) qui relient les sommets. On peut voir un graphe comme une carte géographique : les sommets sont alors des villes et les arêtes sont les routes qui mènent d'une ville à l'autre.

Les graphes sont des objets très pratiques pour étudier les relations entre objets. Par exemple :

• dans un GPS, ils permettent de trouver le plus court chemin entre deux endroits très éloignés (ou le plus touristique, ou celui qui coûte le moins cher en carburant, etc.) ;
• on s'en sert aussi beaucoup en théorie des jeux, où ils permettent aux ordinateurs de trouver une stratégie gagnante  (aux dames, au puissance 4 ou au tic-tac-toe, par exemple) ou, quand c'est impossible, les « meilleurs coups »  (aux échecs, au go, à Othello, etc.) ;
• les réseaux sociaux se comprennent sous la forme de « graphes sociaux » dont les sommets sont les personnes et les arêtes les relations qu'elles entretiennent avec les autres. C'est ce genre de représentation qui permet à la théorie des réseaux sociaux de calculer le prestige d'une personne, la densité du réseau social ou de proposer de nouvelles relations aux utilisateurs ;
• sous l'appellation de flots, ils permettent également de gérer des canalisations, des réseaux téléphoniques, des flux de marchandises, Internet et servent même dans les circuits électriques (lois de Kirchhoff).

La science qui étudie les graphes s'appelle théorie des graphes ; c'est une discipline des mathématiques (en particulier des mathématiques discrètes), de l'algorithmique et de l'informatique.

Définition

Pour pouvoir utiliser les mathématiques, on a défini clairement ce que sont les graphes.

Disons que G est un graphe.

 Mais que pouvons-nous dire de G ? Avec quoi est-il construit ?

G est un ensemble, c'est-à-dire un grand « sac » mathématique qui contient « d'autres choses ». Un peu vague ! Et quelles sont ces choses que contient G ?

Sommets et arêtes

Le réseau routier islandais sous forme de graphe. Les trois graphes sont identiques, même s'ils n'ont, à première vue, pas la même forme : les mêmes sommets ont exactement les mêmes arêtes ! On peut « tordre » un graphe dans tous les sens sans le modifier car la seule chose qui compte, c'est de garder les relations entre les nœuds (« x est relié à y »), c'est-à-dire les arêtes.

On a dit, au début, qu'un graphe était composé de sommets et d’arêtes. G contient donc « les sommets de G » et « les arêtes de G ». Cependant, on ne peut pas mélanger des choses aussi différentes que des sommets et des arêtes dans le même ensemble G. Un ensemble contient des choses qui sont toujours de même nature (ensemble de nombres, par exemple). Or on ne peut pas dire que les sommets sont des arêtes et inversement.

 Alors comment faire pour que G contienne à la fois ses sommets et ses arêtes ?

C'est facile : un ensemble peut contenir d'autres ensembles. Par exemple, l'ensemble des nombres réels contient celui des nombres entiers. On peut donc dire que G contient deux ensembles :

• l'ensemble de ses sommets ;
• l'ensemble de ses arêtes.

Comme cela, tout n'est pas mélangé !

On a l'habitude de noter V l'ensemble des sommets (de l'anglais vertices) et E l'ensemble des arêtes (edges), mais on choisit ici :

• S l'ensemble des sommets ;
• A l'ensemble des arêtes.

Comme G est composé de ses sommets S et de ses arêtes A, on écrit :

G = (S, A)

c'est-à-dire l'ensemble contenant S et A.

Arêtes ou arcs ?

Nous avons parce que les sommets d'un graphe sont reliés entre eux par des « arêtes ». En réalité, tout comme il existe deux types de routes (les routes à sens unique et les routes à double sens), il existe deux types d'« arêtes » :

1. les arêtes à proprement parler, qui sont les liaisons « à double sens ».

   Par exemple, dans un « graphe d'amis », si un sommet s₁ est relié à un sommet s₂, cela signifie que la personne 1 est l'amie de la personne 2. Mais, dans ce cas, il est évident que la personne 2 est aussi l'amie de la personne 1 ! La relation entre s₁ et s₂ est donc à double sens (de s₁ vers s₂ et de s₂ vers s₁). On la représente par un simple trait entre les sommets s₁ et s₂, c'est une arête ;

2. 

   Le « graphe des personnes qui se sont déjà parlé » avec trois sommets et des arcs.
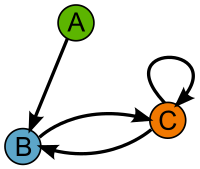
   les arcs sont comme des arêtes « à sens unique ». Ils sont représentés par des flèches. Si l'on a un arc entre deux sommets s₃ et s₄ (avec la flèche pointant vers s₄), cela signifie que s₃ a avec s₄ une certaine relation qui n'est pas forcément réciproque .
   • Par exemple, prenons un « graphe des personnes qui se sont déjà parlé » avec trois sommets (donc trois personnes) A, B et C comme sur l'image à droite. Il existe une flèche (un « arc ») entre A et B, donc Monsieur A a déjà parlé à Monsieur B. Ce n'est pas pour autant que M. B a déjà parlé à M. A ! Il n'y a d'ailleurs pas d'arc reliant B à A. Peut-être que M. B n'a pas entendu que M. A lui parlait. La relation entre A et B est donc « à sens unique » : elle ne va que de A vers B car Monsieur B n'a jamais parlé à Monsieur A.
   • Ce n'est pas parce qu'une relation a un sens (on dit qu'elle est « orientée ») qu'on est toujours dans cette situation de sens unique : on voit sur le graphe que M. B a déjà parlé à M. C (parce qu'une flèche va de B à C) mais il y a également une flèche de C vers B, donc M. C a lui aussi déjà parlé à M. B. On peut donc imaginer que MM. B et C ont eu une conversation.
   • Enfin, on remarque sur le sommet C un arc qui fait une sorte de boucle : il part de C pour revenir vers C. Cela signifie juste que M. C s'est déjà parlé à lui-même.

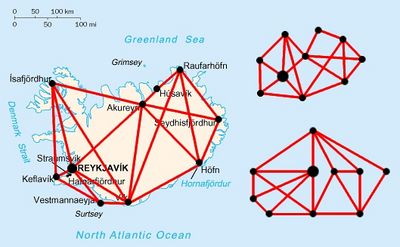
Un graphe ne peut contenir que des arêtes ou que des arcs, pas un mélange des deux. On appelle « graphe orienté » un graphe fait avec des arcs et « graphe non-orienté » un graphe fait avec des arêtes. Le graphe du réseau routier islandais vu à la section précédente est donc non-orienté (pas de flèche, parce qu'on peut circuler sur ces routes dans les deux sens) alors que le « graphe des personnes qui se sont déjà parlé », lui, est orienté.

Poids

Graphe des distances entre quatre grandes villes, en kilomètres.

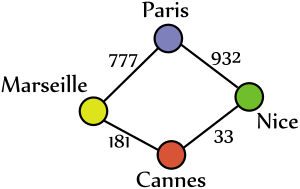
Reprenons l'exemple du GPS : pour lui, les villes sont des sommets et les routes les arêtes qui les relient.

Le chemin le plus court pour aller d'une ville à l'autre est donc celui des « arêtes les plus courtes ». Sauf que, dans un graphe, on dessine les arêtes de la longueur que l'on veut ! Une arête est simplement un moyen de dire « le sommet x est relié au sommet y ». Pourtant, le GPS a besoin de savoir quelle distance sépare deux villes pour calculer le chemin le plus court…

On peut alors donner un poids à chaque arête. Par exemple, on peut dire que le poids de l'arête qui relie les sommets x et y est la distance qui sépare les villes x et y. De cette façon, notre GPS sait que le chemin le plus court est celui qui a le plus petit poids (la plus courte distance). Dans l'image à droite, par exemple, il y a deux moyens d'aller de Nice à Marseille : passer par Paris ou par Cannes. Grâce aux poids, on sait que passer par Paris fait parcourir 932 + 777 = 1709 km, alors que passer par Cannes ne fait parcourir que 181 + 33 = 214 km, ce qui est beaucoup plus court. Le GPS sait alors qu'il est bien plus intéressant de passer par Cannes que par Paris pour aller de Nice à Marseille !

 Où rajouter ces poids dans notre ensemble G ?

Nous avons dit que les arêtes ne sont que des objets qui disent « il existe une relation entre ces deux sommets » : elles ne « portent » pas d'autre information. Nous ne pouvons donc pas stocker les poids « sur » les arêtes.

En revanche, il est parfaitement possible de faire comme pour les sommets et les arêtes : nous n'avons qu'à dire que P est l'ensemble des poids. P a donc la même taille que A (puisque chaque arête a un unique poids) mais il contient des valeurs (ou autre chose !) alors que A contient des arêtes. Et nous complétons notre graphe G :

G = (S, A, P).

En théorie des graphes, on note plus souvent w l'ensemble des poids (de l'anglais weight).

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...