Pi (nombre)
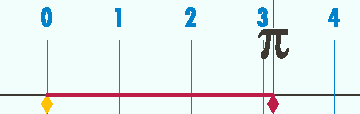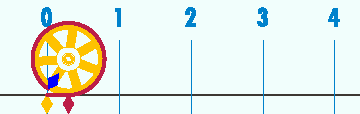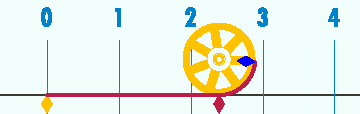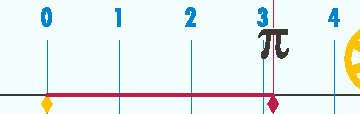
Le nombre pi (d'après la lettre grecque π, initiale de périmètre) est le résultat constant de la division entre la circonférence d'un cercle et son diamètre.
Ce rapport est indépendant de la taille du cercle. C'est un nombre irrationnel, c'est-à-dire qu'il ne peut pas s'écrire comme le résultat d'une fraction dont les deux nombres sont entiers, comme ou par exemple. En particulier, si le diamètre mesure un nombre entier d'unités, la circonférence ne peut pas mesurer un nombre entier d'unités. De plus, on ne peut pas « calculer » puisque ce nombre n'a pas de fin.
est à peu près égal à 3,14 ; mais pour obtenir une meilleure approximation, il faut ajouter encore plus de chiffres derrière la virgule, sans jamais obtenir un résultat exact : on a déjà trouvé plus de 12 000 milliards de chiffres après la virgule en 2013, et cela peut continuer indéfiniment puisque pi n'a pas de fin et que la suite de ses décimales est imprévisible (on ne peut pas savoir à l'avance quel chiffre apparaîtra sans faire de calculs, ou sans apprendre la suite par cœur). Une valeur plus approchée en est 3.14159265359.
Le nombre π apparait aussi dans l'expression de l'aire d'un disque. On retient :
et :
Histoire[modifier | modifier le wikicode]
Avant notre ère, les Babyloniens (civilisation située à l'est de l'Euphrate (un fleuve), entre 2000 et 1000 av J.C.) trouvent que Pi correspond à peu près à 3.
Vers 250 av J.C., Archimède, un savant grec (vers 278 av. J.C. vers 212 av J.C), à la fois mathématicien, géomètre, physicien et ingénieur, a calculé Pi par la méthode des polygones réguliers.
Au IIIe siècle, en Chine on parvient à déterminer que Pi correspond à 3,14159.
En 500, le mathématicien Hindou Haryabata propose 3,1416 et redécouvre les décimales trouvées par Archimède.
En 1593, le français François Viète, juriste (les mathématiques ne furent pour lui qu'un passe temps) donnera 11 décimales exactes.
En 1596, Louis de Cologne calcule les 20 premières décimales de Pi .
Le symbole de Pi n'est apparu que vers 1600 et c'est un mathématicien suisse nommé Leonhard Euler qui impose cette écriture au milieu du XVIIIe siècle.
En 2002, le Japonais Yasumasa Kanada calcule jusqu’aux 1 241 100 000 000 décimales de Pi.
Utilisation[modifier | modifier le wikicode]
On utilise le nombre Pi en algèbre ou en géométrie. Le nombre Pi intervient dans presque tous les domaines des mathématiques (trigonométrie, nombre complexe, exponentielles, statistiques, etc.). Pi est utilisé également en physique et en astronomie.
La suite des décimales de Pi est utilisée pour tester le fonctionnement des ordinateurs. Il peut notamment être utilisé pour générer un nombre de manière pseudo-aléatoire, les décimales de Pi n'étant pas régulières.
Sans ce nombre, on pourrait difficilement construire des voitures, comprendre le mouvement des planètes ou fabriquer des ballons.
Ce qui est incroyable avec Pi, c’est que sa valeur reste toujours la même, quelle que soit la taille du cercle, de la planète ou du ballon.
Mémoire[modifier | modifier le wikicode]
Il existe un moyen mnémotechnique pour se souvenir des premières décimales avec ce vers, le nombre de lettres dans chaque mot donnant le chiffre correspondant :
- Que j'aime à faire apprendre un nombre utile aux sages. Immortel Archimède, artiste ingénieur, Qui de ton jugement peut priser la valeur ?
- Que (3) j' (1) aime (4) à (1) faire (5) apprendre (9) un (2) nombre (6) utile (5) aux (3) sages (5)…
Le savais-tu ?
| ||
| Les calculs de pi d'Archimède | ||
| Au IIIe siècle av. J-C, Archimède, un grand scientifique de la Grèce antique, a réussi à trouver une approximation de PI en métrique L² (euclidienne) très précise:
223/71 < < 22/7
soit 3,14084507 < < 3,14285714 Comment a-t-il fait ? En fait, rien de sorcier: il a tracé plusieurs figures (polygones réguliers) et a comparé leur périmètre à celui du cercle (cercle inscrit ou cercle circonscrit). Archimède a procédé ainsi jusqu'à une figure de 96 côtés ! | ||
Culture populaire[modifier | modifier le wikicode]
La journée de pi est fêtée chaque année le 14 mars. En effet, en américain, « 14 mars » s'écrit « 3/14 ». C'est cette ressemblance avec 3,14 qui fait que ce jour a été choisi. Cependant, depuis 2013, l'association Pi Day organise à titre bénévole de nombreux événements de diffusion scientifique grand public, dont la Tournée de π, sa plus célèbre. Des conférences, des comédies musicales, etc...
Voir aussi[modifier | modifier le wikicode]
- la mémorisation de pi
- Le Nombre d'or, un autre nombre très particulier.
|
|
|
Autres articles fruits d'un travail scolaire |