Triangle équilatéral
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur. Autrement, un triangle équilatéral ABC, c'est trois points A, B et C du plan tels que AB = BC = CA. Non seulement les trois côtés ont la même longueur, mais de plus les trois angles ont la même mesure : 60° ni plus, ni moins.
Éthymologie : L'adjectif équilatéral provient du latin aequus (égal) et latus (côté). Donc, équilatéral signifie exactement d'égal côté.
Angles[modifier | modifier le wikicode]
- Un triangle est équilatéral si, et seulement si, ses trois angles sont égaux.
Un triangle équilatéral ABC vérifie par définition AB=AC=BC. En particulier, il est isocèle en A ; en B et en C. Comme il est isocèle en A, les angles en B et en C sont égaux. Comme il est isocèle en B, les angles en A et en C sont égaux. Ses trois angles sont donc égaux.
Réciproquement, si les trois angles de ABC sont égaux, alors il est isocèle en A ; en B et en C. Donc, AB=AC ; BA=BC et CA=CB. Par conséquent, les trois côtés ont mêmes longueurs.
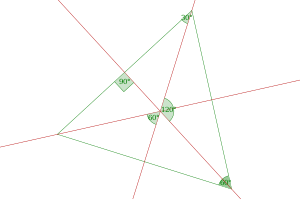
- La hauteur et la bissectrice issues d'un des sommets, la médiane de l'angle en ce sommet, et la médiatrice du segment opposé sont quatre droites confondues.
- Dans un triangle équilatéral, l'orthocentre, le centre du cercle circonscrit, et le centre du cercle inscrit sont trois points confondus.
L'orthocentre est l'intersection des trois hauteurs du triangle ; le centre du cercle inscrit est l'intersection des trois médianes ; le centre du cercle circonscrit est l'intersection de ses trois médiatrices. Médiatrices, médianes et hauteurs se confondent dans un triangle équilatéral.
Hauteur et aire[modifier | modifier le wikicode]
La hauteur d'un triangle équilatéral est égale à la longueur que l'on multiplie par la moitié de la racine carrée de 3.
L'aire d'un triangle équilatéral de côté a vaut a² × sqrt (3) /4
Construction d'un triangle équilatéral[modifier | modifier le wikicode]
| Sur la géométrie du triangle | |
|---|---|
|