Racine carrée

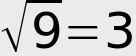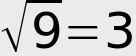
La racine carrée de neuf est égale à trois (notation mathématique)

La racine carrée d'un nombre réel positif est l'unique nombre positif qui, lorsqu'il est multiplié avec lui-même, redonne le nombre réel de départ.

Par exemple, la racine carrée de 9 est 3 parce que 3 × 3 = 9. On note formellement : √9 = 3.

Le symbole √ dérive de la lettre r. La notation √9 peut se lire « racine de 9 » ; « racine carrée de 9 » ou encore « radical de 9 ».

Carré parfait

La lecture des tables de multiplication permettent de fournir des racines carrées remarquables :

• $2\times 2=4$ donne ${\sqrt {4}}=2$ ;
• $3\times 3=9$ donne ${\sqrt {9}}=3$ ;
• $4\times 4=16$ donne ${\sqrt {16}}=4$ ;
• $5\times 5=25$ donne ${\sqrt {25}}=5$ ;
• $6\times 6=36$ donne ${\sqrt {36}}=6$ ;
• $7\times 7=49$ donne ${\sqrt {49}}=7$ ;
• $8\times 8=64$ donne ${\sqrt {64}}=8$ ;
• $9\times 9=81$ donne ${\sqrt {81}}=9$ ;
• etc.

Un carré parfait est un entier naturel qui est le carré d'un autre. 1, 4, 9, 16, 25, 36, … sont les premiers carrés parfaits, car 1²= 1, 2² = 4, 3² = 9… La diagonale d'une table de multiplication fournit la liste des premiers carrés parfaits.

Question : Comment trouver les carrés parfaits ?

Parmi les entiers naturels 144, 442, 784 et 1424, lesquels sont des carrés parfaits ? Et quelles sont leurs racines carrées ?

Réponses

La stratégie consiste à chercher des entiers dont les carrés sont proches de 144, 442, 784, 1424 et 2809. Si un entier est strictement compris entre les carrés de deux entiers consécutifs, il ne peut pas être un carré parfait.

• 144 est un carré parfait car 12 × 12 = 144 ; la racine carrée de 144 est 12.
• 442 n'est pas un carré parfait car 21 × 21 = 441 et 22 × 22 = 484.
• 784 est un carré parfait car 28 × 28 = 784 ; la racine carrée de 784 est 28.
• 1424 n'est pas un carré parfait car 37 × 37 = 1369 et 38 × 38 = 1444.
• 2809 est un carré parfait car 53 × 53 = 2809 ; la racine carrée de 2809 est donc 53.

Irrationnalité

Oui, mais pour un entier quelconque ? Tous les nombres plus grands que zéro ont une racine carrée ! Seulement, pour la trouver, il faut chercher des nombres qui ne sont pas entiers (des nombres avec une virgule). Par exemple, la racine carrée de 20 est environ égale à 4,47213595499957939..., c'est-à-dire un nombre proche de 4 et demi.

La racine carrée d'un entier qui n'est pas un carré parfait ne peut pas être mis sous la forme d'une fraction. On dit que c'est un irrationnel. En particulier, son développement n'est pas périodique.

Calculer une racine carrée

Quelques valeurs de racines carrées :

• ${\sqrt {1}}=1$
• ${\sqrt {2}}=1,41421356237309504880\ldots$ (voir l'article Racine carrée de 2)
• ${\sqrt {3}}=1,73205080756887729352\ldots$
• ${\sqrt {4}}=2$
• ${\sqrt {5}}=2,23606797749978969640\ldots$
• ${\sqrt {6}}=2,44948974278317809819\ldots$

Équations du second degré

Les racines carrées interviennent pour résoudre les équations polynômiales du second degré.

Par exemple, on veut résoudre $x^{2}+6x-3=0$ où $x$ est une inconnue :

$(x+3)^{2}-12=0$ ;

$(x+3)^{2}=12$ ;

donc $x$ vaut $-3+{\sqrt {12}}$ ou $-3-{\sqrt {12}}$

De manière générale :

La solution générale d'une équation $Ax^{2}+Bx+C=0$ est :

$x={\frac {-B+{\sqrt {\Delta }}}{2A}}$ ou $x={\frac {-B-{\sqrt {\Delta }}}{2A}}$

où $\Delta =B^{2}-4\cdot A\cdot C$ est le discriminant du polynôme $Ax^{2}+Bx+C$.

Par exemple, si on veut résoudre $2x^{2}-3x+{\frac {7}{8}}=0$ où $x$ est une inconnue :

On calcule $\Delta =(-3)^{2}-4\cdot 2\cdot {\frac {7}{8}}=2$

On calcule ensuite $x={\frac {-(-3)+{\sqrt {2}}}{2\cdot 2}}$ ou $x={\frac {-(-3)-{\sqrt {2}}}{2\cdot 2}}$

En réduisant, on trouve $x={\frac {3+{\sqrt {2}}}{4}}$ ou $x={\frac {3-{\sqrt {2}}}{4}}$

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...