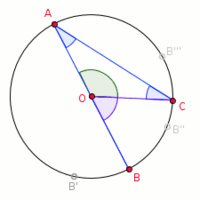
Angle au centre et angle inscrit

Dans un cercle $\scriptstyle {\mathcal {C}}$ :

• Un angle au centre est un angle formé par deux rayons ;
• Un angle inscrit est l'angle formé par deux cordes.

Dans la figure ci-contre, $A$, $B$ et $C$ sont trois points du cercle ${\mathcal {C}}$ de centre $O$. L'angle ${\widehat {BOC}}$ est un angle au centre. ${\widehat {BAC}}$ est un angle inscrit.

Théorème de l'angle inscrit et de l'angle au centre

Dans un cercle l'amplitude d'un angle au centre vaut le double de l'amplitude d'un angle inscrit qui intercepte le même arc. Sur la figure, pour l'arc $BC$ : ${\widehat {BOC}}=2\times {\widehat {BAC}}$

Démonstration

A, O, B alignés. AÔB = 180°
Alors 2 × CÂB = CÔB

A, O, M alignés.
Alors … 2 × CÂB = CÔB

En mathématiques comme en sciences, on avance une première hypothèse d'après des observations. On observe que le résultat précédent est vérifié dans un grand nombre de situations. Tu peux faire des dessins sur une feuille blanche, avec un compas et une règle, et utiliser un rapporteur pour mesurer les angles. Cependant, pour pouvoir affirmer que ceci est vrai, il faut le démontrer.

Première étape

Supposons A et B diamétralement opposés. Par conséquent, O est le milieu de [AB] , A , O et B sont alignés, l'angle AÔB vaut 180°. La somme des angles AÔC et CÔB vaut 180°.
Le triangle AOC étant isocèle en O donc OÂC = OĈA. Et comme pour tout triangle la somme des angles vaut 180° : 2 × OĈA + AÔC = 180° .
Donc, 2 × OĈA = 180 – AÔC = CÔB et comme CÂO = CÂB puisque A , O et B sont alignés, 2 × CÂB = CÔB .
(De ceci on peut aussi facilement déduire qu'AĈB = 90° : triangle rectangle inscrit dans un cercle.)
Cette étape va nous aider pour la suite de la démonstration :

Seconde étape

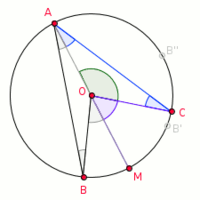
Reprenons le cas général du schéma en début d'article.
On va ajouter un point M au cercle, de manière qu'O soit le milieu de [AM] : À , O et M sont alignés, etc. On a donc avec M les résultats de la première étape, avec M à la place de B.
Il suffit alors d'ajouter (ou de soustraire, selon où se trouvent B par rapport à C sur le cercle), la propriété démontrée dans la première étape pour démontrer la propriété dans le cas général.
En effet CÂB = CÂM + MÂB et CÔB = CÔM + MÔB ,
(Pour B' entre C et M : CÂB' = CÂM – MÂB' et CÔB' = CÔM – MÔB' . Pour C entre B” et M, CÂB” = MÂB” – CÂM et CÔB” = MÔB” – CÔM).

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...