Rectangle

Un rectangle tracé à la main

Il existe un quiz sur le rectangle.

Un rectangle est un quadrilatère qui possède quatre angles droit.

Propriétés

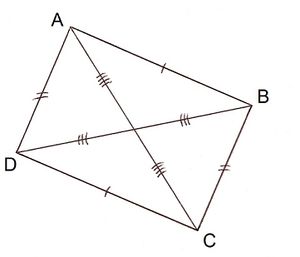
Dans un rectangle ABCD,

• Les quatre angles sont droits ;
• Les côtés opposés sont parallèles et ont les mêmes longueurs ;
• Les côtés opposés ont la même médiatrice ;
• Les diagonales et les médiatrices s'intersectent en leurs milieux ;
• Ce point d'intersection O est un centre de symétrie ;
• Les médiatrices sont des axes de symétrie.

Définitions équivalentes

• Un quadrilatère qui possède trois angles droits est un rectangle.
• Un quadrilatère dont les diagonales ont la même longueur et s'intersectent en leur milieu est un rectangle.

Périmètre et aire

• L'aire d'un rectangle dont les côtés ont pour longueurs a et b est : $a\times b$.
• La formule du périmètre est : $P=2(L+l)=2L+2l$

Exemple : Un rectangle fait 8 cm de longueur sur 3 de largeur :

• Aire : $8\times 3=24cm^{2}$.
• Périmètre : $2(8+3)=11\times 2=22cm$.

Questions :

• Pour quels rectangles l'aire est supérieure à l'aire de tout rectangle de même périmètre ?
• Pour quels rectangles le périmètre est-il inférieur au périmètre de tout rectangle de même aire ?

Réponses : Dans les deux cas, les carrés !

• Si un rectangle de côtés de longueur a et b a pour périmètre 2d, alors $b=d-a$. Donc, son aire vaut $a(d-a)$. Par l'inégalité arithmético-géométrique, l'aire est inférieure à ${\frac {d^{2}}{4}}$. et strictement inférieure si a et $b=d-a$ sont inégaux.

• Si un rectangle de côtés de longueur a et b a pour aire A, alors $b={\frac {A}{a}}$. Donc son périmètre vaut ${\frac {A+a}{a}}$ ; il est inférieur à $2{\sqrt {A}}$, et est strictement inférieur si a et b sont inégaux.

Liens internes

• Condition nécessaire

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...