Preuve de Garfield
La preuve de Garfield est une démonstration du théorème de Pythagore, qui a été redécouverte par le président américain James Abraham Garfield. Néanmoins, elle était connue au Ve siècle av. J-C.
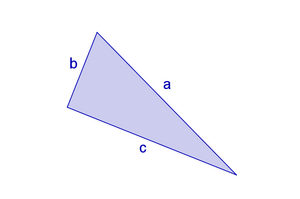
D'après le théorème de Pythagore, dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres longueurs. Dans la figure ci-contre, on a tracé un triangle ABC rectangle en A. Le théorème de Pythagore dit que :
Cet article fournit une démonstration connue de ce théorème.
Première « preuve »[modifier | modifier le wikicode]
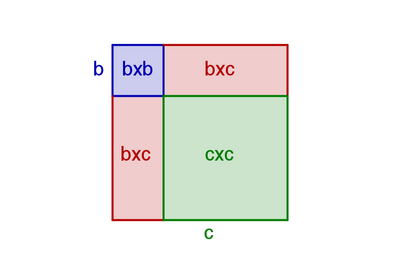
Sur la figure ci-à droite, on a représenté un carré dont le côté a pour longueur b + c. En traçant des droites parallèles aux côtés du carré, on a pu diviser ce carré en deux rectangles et deux carrés :
- Le carré bleu a pour côté b ; son aire est b2 ;
- Les rectangles rouges ont pour longueurs b et c. Ils ont donc pour aire b×c ;
- Le carré vert a pour côté c ; son aire est c2.
(Rappelons que l'aire d'un rectangle est effectivement le produit de ses deux longueurs.) Comme l'aire est « additive », l'aire du carré s'obtient en ajoutant les aires des deux rectangles et deux carrés qui le composent. Elle vaut donc :
(Ne pas oublier le facteur 2 car il y a deux rectangles rouges.) Mais la longueur du côté du grand carré est connue : elle vaut b + c. Par conséquent :
(C'est une des identités remarquables.)
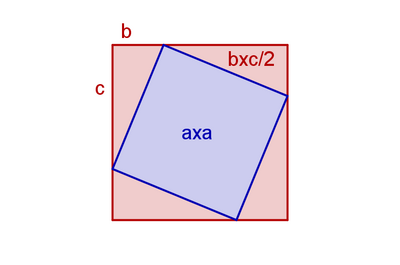
Sur la figure à droite, on a repris le carré de côté b + c. On l'a divisé d'une autre façon.
- Le côté du carré bleu a pour longueur a ;
- Les quatre triangles rouges ont les mêmes longueurs : leurs petits côtés mesurent b et c.
Le carré a donc pour aire :
On obtient alors :
Après simplification par 2×b×c, il vient :
(On n'a pas justifié la construction des deux figures, mais c'est un bon exercice de les reproduire sur une feuille par soi-même.)
Histoire[modifier | modifier le wikicode]
Le président américain Garfield a proposé cette démonstration. C'est pourquoi elle lui est attribuée en Europe et en Amérique du Nord. Cependant, en Asie, cette preuve avait été trouvée vers le IIIe siècle de notre ère. La redécouverte par Garfield est indépendante, car au XIXe siècle, les mathématiques chinoises étaient méconnues aux États-Unis.
Par ailleurs, on note des progrès scientifiques croissants en Europe depuis la Renaissance, et tout particulièrement aux XVIIIe et XIXe siècles. Ces progrès en mathématiques furent pour l'essentiel ignorés en Asie.
Il se peut que la démonstration ci-dessus soit connue avant, mais aucune trace écrite n'en a été retrouvée. Néanmoins, au moins une démonstration du théorème de Pythagore fut connue par Euclide et on disposait de preuves différentes et indépendantes en Inde et en Chine durant « l'Antiquité ».
|