Théorème de Pythagore

Le théorème de Pythagore est un théorème fondamental de trigonométrie découvert par Pythagore. Il énonce une relation entre les longueurs des trois côtés d'un triangle rectangle. Un triangle rectangle est un triangle qui présente un angle droit. Le côté opposé à l'angle droit s'appelle l'hypoténuse. Ce théorème était connu aussi des chinois, des babyloniens et dans d'autres cultures 1000 ans avant Jésus-Christ.

Un triangle rectangle, illustration pour comprendre le théorème de Pythagore

Le théorème de Pythagore affirme :

Dans un triangle rectangle, le carré de la longueur de l'hypoténuse (côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des deux autres côtés.

Le Théorème de Pythagore explique que si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Soit le triangle ABC rectangle en A ci-contre. D'après le théorème de Pythagore, on a : BC² = AB² + AC².

Pour calculer une longueur dans un triangle rectangle, la rédaction est très importante.

Nous commençons par dire que le triangle est rectangle. Nous citons d'hypoténuse, nous citons le théorème de Pythagore, puis la version littérale du théorème, après nous remplaçons les valeurs littérales par les valeurs réelles, et nous calculons (exemple ci-dessous en prenant l'exemple simple de : CA=3cm; AB=4cm).

Le triangle ABC ci-contre est rectangle en A.

Son hypoténuse est [CB]

Selon le théorème de Pythagore : CB²=CA²+AB²

Donc : CB²= (3cm)²+(4cm)²

= 9cm + 16 cm

=25cm

Donc CB²=25cm

Maintenant, nous connaissons CB², mais nous cherchons cependant CB, et pas CB². Pour trouver CB, nous allons utiliser la racine carré pour faire l'inverse du carré et faire devenir CB² en CB. Donc nous faisons √25; ce qui donne 5. l'hypoténuse [CB] est donc égal à 5cm.

Si vous voulez utiliser le théorème de Pythagore autrement, je vous invite à regarder cette illustration dans cette vidéo traitant du théorème de Pythagore.

Il est remarquable que les trois longueurs sont un nombre entier de centimètres. Si la somme des carrés de deux entiers est le carré d'un troisième, ces trois entiers s'appellent triplet pythagoricien. Par exemple, (3;4;5 ou 6,8;10) est un triplet pythagoricien.

Interprétation géométrique

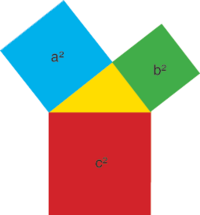
À droite, on a représenté un triangle rectangle, et on a construit trois carrés sur chaque côté du triangle :

• Le carré rouge est construit sur l'hypoténuse du triangle rectangle. Son aire (surface !) est le carré de l'hypoténuse, elle vaut c².
• Les carrés bleu et vert sont construits sur les deux petits côtés. Leurs aires sont a² et b².

Le théorème de Pythagore affirme que la somme des aires des carrés bleu et vert vaut exactement l'aire du carré rouge. Ici, on a donné une interprétation géométrique de la somme :

c²  =   a²  +  b².

Une méthode pour démontrer le théorème de Pythagore est la suivante. On découpe le carré rouge en pièces élémentaires (petits carrés, triangles, trapèzes, autres) ; on mélange les pièces et on les recolle pour former les deux carrés vert et bleu. Attention, il faut que le découpage proposé puisse être réalisé avec n'importe quel triangle rectangle. Il ne faut pas ajouter non plus de surface et se contenter de déplacer les pièces.

Un découpage possible.

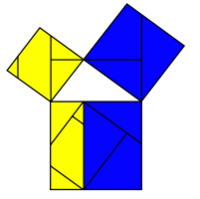
L'image à gauche montre un découpage possible. C'est un excellent exercice de comprendre comment se réalise le découpage, et de le présenter ensuite à ses camarades.

• La hauteur issue du sommet de l'angle droit va découper le grand carré en deux rectangles : à gauche, le rectangle jaune, et à droite, le rectangle bleu.
• Le rectangle bleu est découpé en trois pièces (deux triangles et un quadrilatère) qui sont ensuite associées pour former le carré bleu.
• Le rectangle jaune est découpé en quatre pièces qui sont aussi associées pour former le carré jaune.

Sur la figure, on « voit » que les pièces se correspondent. Pour démontrer que les polygônes se correspondent deux à deux, il faut calculer leurs angles, qui doivent être les mêmes, puis calculer au moins une longueur. Il faut donc faire des calculs d'angles et de longueurs pour conclure (on ne va pas le faire, mais c'est un très bon exercice).

Des carrés et un triangle rectangle.

Animation : Triangle rectangle. Le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.

Histoire

Le théorème de Pythagore doit son nom au mathématicien grec Pythagore. Toutefois, il n'existe aucun écrit de Pythagore. Il aurait vécu à Crotone au sud de l'actuelle Italie et y aurait fondé une école, l'école des pythagoriciens. De nombreux résultats élémentaires de géométrie leur sont attribués.

Toutefois, le théorème de Pythagore était connu par des civilisations antérieures à la civilisation grecque. Les scribes assyriens et babyloniens réalisaient des exercices de mathématiques sur des tablettes d'argile séchées. On en a retrouvés beaucoup en Irak et en Iran. Ces tablettes concernent des problèmes d'arithmétique, parfois des exercices de géométrie. Seuls les triangles rectangles étaient étudiés, et les scribes savaient calculer des longueurs inconnues. Ils utilisaient le théorème de Pythagore (on ignore s'ils en connaissaient la preuve). Par ailleurs, les scribes avaient aussi développé des méthodes pour trouver des triplets pythagoriciens.

La première preuve écrite du théorème de Pythagore date du IV^e siècle av. J-C C'est Euclide qui l'a donnée dans le livre I de ses Éléments : c'est une œuvre majeure dans l'histoire des mathématiques. On connaît son contenu par une traduction arabe.

Une deuxième preuve du théorème a été donnée en Chine dans le Zhoubi suanjung vers le II^e siècle av. J-C (la date est incertaine). Le théorème est appelé en Asie théorème de Gougu. Cette preuve est sensiblement différente de celle d'Euclide. Il est vraisemblable que les deux preuves ont été données indépendamment.

Au IX^e siècle, le mathématicien de langue arabe Al Kashi généralisa le théorème de Pythagore : il énonça le théorème dit d'Al Kashi. Ce théorème donne une relation entre les longueurs des trois côtés d'un triangle quelconque et la mesure d'un de ses angles.

Démonstrations

La plupart des démonstrations du théorème de Pythagore s'appuient sur une préservation des aires.

La démonstration de Garfield

• Voir Preuve de Garfield

Le vingtième président des États-Unis d'Amérique, James Garfield, a donné une démonstration du théorème. Considérons ABC un triangle rectangle en A. On note :

AB = c ; AC = b ; BC = a.

Le triangle rectangle ABC s'inscrit dans un carré AFGH de côté b + c, de sorte que :

• Le point B appartient au segment [AF] ;
• Le point C appartient au segment [AH].

On introduit les points :

• Le point D du segment [FG] tel que FD = c ;
• Le point E du segment [GH] tel que GE = c.

La figure présente une certaine symétrie. Le centre du carré est le centre d'une rotation qui envoie ABC sur FDB, FDB sur GED, GED sur HCE et enfin HCE sur ABC. En particulier, les angles aux sommets sont égaux. Comme la somme des angles d'un triangle vaut 180°, les angles du quadrilatère CBDE sont droits. Par ailleurs, ses côtés ont même longueur.

Autrement dit, le quadrilatère CBDE est à la fois un rectangle et un losange : c'est donc un carré. L'additivité de l'aire implique :

2b · c + a² = (b + c)².

En développant le terme de droite, il vient :

a² = b² + c².

Autrement dit, le carré de l'hypoténuse est égal à la somme des carrés des côtés de l'angle droit, comme annoncé.

La démonstration d'Euclide

Cette section est vide, pas assez détaillée ou incomplète. Améliore-la !

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...

Article mis en lumière la semaine du 24 septembre 2018.