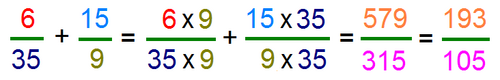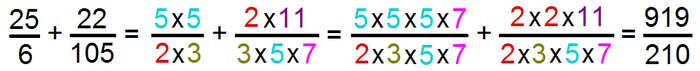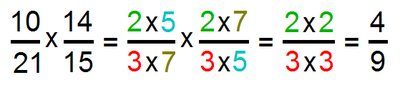Fraction
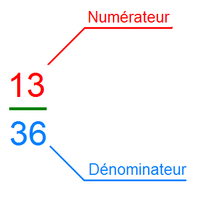
En mathématiques, une fraction représente une division (un quotient). Il s'agit du rapport ou de la proportion entre deux nombres : le numérateur (celui qui est divisé) et le dénominateur (celui qui divise). Pour retenir ces noms, on peut penser à « NUage » pour le numérateur, étant au dessus de la barre de fraction, et à dessous, le dénominateur étant en dessous.
Vocabulaire[modifier | modifier le wikicode]
Une fraction s'écrit par une barre horizontale et deux entiers :
- Le premier entier se place au-dessus de la barre ; il s'appelle le numérateur ;
- Le second entier se place au-dessous de la barre ; il s'appelle le dénominateur.
Dans l'exemple ci-contre, 13 est le numérateur et 36 le dénominateur. On lit la fraction treize sur trente six ou treize trente-sixièmes. Que représente cette fraction ? C'est le quotient de 13 par 36.
Expression d'une fraction[modifier | modifier le wikicode]
Prenons la fraction . On peut la lire 1 divisé par 2, un demi ou encore .
Notons qu'il est aussi possible de l'écrire avec une barre oblique au lieu de la barre horizontale : .
- Si le dénominateur est 1, on dit 1 unité, ou on ne dit que le numérateur (5/1 = cinq unités) ;
- Si le dénominateur est 2, on dit demi (1/2 = Un demi) ;
- Si le dénominateur est 3, on dit tiers (1/3 = Un tiers) ;
- Si le dénominateur est 4, on dit quart (1/4 = Un quart) ;
- Si le dénominateur est supérieur à 4, on utilise le nombre ordinal (1/5 = Un cinquième, 5/147 = Cinq cent-quarante-septième).
Comparaison de fractions par rapport à 1[modifier | modifier le wikicode]
- Si le dénominateur est plus grand que le numérateur, la fraction est inférieure à 1.
- Si le dénominateur est plus petit que le numérateur, la fraction est supérieure à 1.
- Si le dénominateur est égal au numérateur, la fraction vaut 1, on peut aussi dire un entier1.
Fractions équivalentes[modifier | modifier le wikicode]
Prenons la fraction : Cette fraction est équivalente à
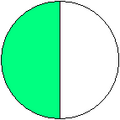
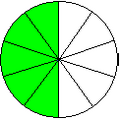
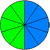
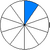
En effet, on a cinq divisé par dix, soit cinq dixièmes : . Il faut bien comprendre ici que le rapport reste le même. Voyez les deux schémas ci-contre pour bien comprendre : le premier représente un demi, l'autre cinq dixièmes.
En multipliant (ou en divisant) le numérateur et le dénominateur par un même nombre, on conserve le même rapport.
On peut exprimer des fractions avec une ligne numérique
Ici on représente des dixièmes. En bleu, les nombres entiers, en noir les fractions. On notera que dix dixièmes valent un, vingt dixièmes valent deux, etc.
Les fractions permettent aussi d'exprimer des pourcentages, on utilise pour cela un dénominateur qui est égal à 100. Par exemple, pour parler du 25% d'une population, on peut écrire la fraction .
On peut lire cette fraction comme « 25 personnes sur 100 ». Mais il est possible de simplifier (ou réduire) cette fraction (voir plus bas pour l'explication technique) afin d'obtenir 1/4 (« un quart »). En effet, dire « 25% d'une population » est équivalent à dire « un quart de la population ».
Simplification[modifier | modifier le wikicode]
Une fraction peut être simplifiée en divisant le numérateur et le dénominateur par le plus Grand Commun Diviseur. Par exemple, les deux fractions suivantes sont équivalentes :
On a utilisé ici le plus grand diviseur commun de 4 et de 10, qui est 2. On ne peut pas simplifier davantage cette fraction, on dit donc qu'elle est irréductible.
Pour rendre irréductible une fraction, on peut décomposer le numérateur et le dénominateur en produit de facteurs premiers puis simplifier la fraction.
Opérations avec les fractions[modifier | modifier le wikicode]
Il est possible d'effectuer plusieurs opérations mathématiques avec les fractions.
Additionner des fractions[modifier | modifier le wikicode]
Pour additionner plusieurs fractions, il faut que leurs dénominateurs soient équivalents. C'est pourquoi il est très souvent nécessaire de les réduire au même dénominateur. Pour ce faire, il faut trouver un nombre multiple de chacun des dénominateurs, et multiplier les numérateur respectivement par le nombre par lequel nous avons multiplié le dénominateur, afin de conserver des fractions équivalentes.
Pour trouver un dénominateur commun, il est préférable de factoriser dans un premier temps les dénominateurs :
Exemple[modifier | modifier le wikicode]
Nous allons calculer la somme suivante :
Pour additionner 1/2 et 3/5, il faut d'abord calculer le dénominateur commun entre 2 et 5. Ici, on peut prendre 10, car celui-ci est divisible par 2 et par 5 ; de plus, il s'agit du plus petit commun multiple. Il est toujours préférable de prendre le plus petit commun multiple afin d'éviter d'avoir à multiplier par de grands nombres.
Il faut ensuite multiplier le numérateur de chacune des fractions par le même nombre que le dénominateur, afin que le rapport reste le même. Dans le cas de 1/2 par exemple, le dénominateur ayant été multiplié par 5 (afin d'obtenir 10, souvenez-vous), il faudra également modifier le numérateur par 5. Nous obtenons donc 5/10 qui est bien équivalente à 1/2.
Il ne reste plus qu'alors à additionner les numérateurs entre eux afin d'obtenir la réponse finale :
Ceci est la seule manière exacte d'obtenir le résultat correct. Additionner les dénominateurs entre eux et les numérateurs entre eux est incorrect. Regardez l'addition suivante :
Soustraire des fractions[modifier | modifier le wikicode]
La soustraction se fait de la même manière que l'addition en utilisant le dénominateur commun, sauf que l'on soustrait les numérateurs.
Multiplier des fractions[modifier | modifier le wikicode]
La multiplication est très simple, il suffit de multiplier le numérateur de la première fraction avec celui de la deuxième fraction, et de multiplier le dénominateur de la première fraction avec le dénominateur de la deuxième fraction.
Exemple :
En simplifiant les numérateurs et dénominateurs, il est possible d'obtenir directement la fraction simplifiée.
Diviser des fractions[modifier | modifier le wikicode]
La division ressemble à la multiplication. Cependant, il faut inverser la deuxième fraction.
Diviser par un nombre revient à multiplier par son inverse.
On voit ici que le a été inversé pour obtenir .
|