Division (mathématiques)
La division est une des quatre opérations élémentaires. Elle permet de faire des partages ou des répartitions. Le résultat d'une division s'appelle le quotient.
La division est la réciproque de la multiplication (le contraire d'une multiplication).
Attention, la division par 0 n'est pas définie ! C'est-à-dire que le calcul est impossible.
Notation[modifier | modifier le wikicode]
Pour noter l'opération, il existe trois symboles différents :
- : est le symbole le plus utilisé à l'école élémentaire en France.
- ÷ se lit le plus souvent sur les calculatrices.
- / est également utilisé, notamment en informatique.
Tous les trois se lisent divisé par. Exemple, 20:5 se lit vingt divisé par cinq.
Un peu de vocabulaire[modifier | modifier le wikicode]
La division fait apparaitre trois nombres :
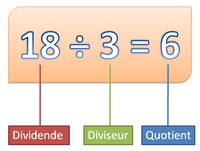
- Le nombre qui est divisé s'appelle le dividende ;
- Le nombre qui divise s'appelle le diviseur ;
- Le résultat de l'opération s'appelle le quotient.
Dans ; 18 est le dividende ; 3 est le diviseur ; et enfin, 6 est le quotient (de 18 par 3).
Exemple[modifier | modifier le wikicode]
Pour prouver qu'une division est correcte, on peut utiliser l'écriture euclidienne. Par exemple, avec reste . Voici l'écriture euclidienne :
. Donc la division est correcte.
À quoi cela sert-il ?[modifier | modifier le wikicode]
On distingue deux cas, le partage et la répartition.
Le partage[modifier | modifier le wikicode]
On peut utiliser la division pour faire un partage équitable. Par exemple, cinq enfants se partagent vingt bonbons. On divise les vingt bonbons par cinq : 20:5=4, chaque enfant reçoit 4 bonbons.
Et que se passe-t-il s'il y a 21 bonbons ? Chaque enfant reçoit 4 bonbons, et il reste un qu'on ne peut pas partager. On écrira avec reste 1.
La répartition[modifier | modifier le wikicode]
La situation est légèrement différente. La répartition consiste à faire des groupes égaux. Par exemple, 42 personnes veulent jouer au handball. Ils font des équipes de 7 joueurs. Combien d'équipes peuvent-ils composer ? , il y aura 6 équipes de 7 joueurs.
Et que se passe-t-il s'ils sont 44 ? Eh bien, il restera 2 joueurs sans équipe. Cela tombe bien, il faut des remplaçants !
Un peu plus difficile : Chaque mouton a quatre pattes et zéro aile ; chaque poule a deux pattes et deux ailes. Dans une ferme, il n'y a que des poules et des moutons. Je compte 26 ailes et 122 pattes. Combien y-a-t-il de moutons ?
Comment faire une division ?[modifier | modifier le wikicode]
Grâce à la soustraction[modifier | modifier le wikicode]
Reprenons le cas de nos joueurs de handball. Ils sont 42. On peut prendre chaque fois 7 joueurs pour faire une équipe. Quand tout le monde est dans une équipe, on s'arrête. En mathématiques, on écrira :
On a pu composer six équipes (on a enlevé 6 fois 7 joueurs des 42 personnes).
Grâce à la multiplication[modifier | modifier le wikicode]
La soustraction, cela fonctionne, mais ce n'est pas très pratique. On peut également utiliser la multiplication, puisque c'est la réciproque de la division. Pour cela, il faut bien connaître ses tables !
Prenons un nouvel exemple. Six enfants doivent se partager la somme de 24 €.
- Si chaque enfant reçoit 1 €, , on a partagé 6 €, on peut continuer.
- Si chaque enfant reçoit 2 €, , on a partagé 12 €, on peut continuer.
- Si chaque enfant reçoit 3 €, , on a partagé 18 €, on peut continuer.
- Si chaque enfant reçoit 4 €, , on a partagé 24 €, c'est fini !
Bien entendu, avec l'habitude, on voit tout de suite que 24 est dans la table de 6, et on va beaucoup plus vite. Et si on partage 14 € entre ces six enfants ?
- On ne peut pas donner 3 € à chacun, il en faudrait 18 !
- On en donne donc 2, ce qui fait 2x6=12. On a partagé 12 € et il en reste 2. Pour aller plus loin, il faudrait partager les centimes.
Qu'est-ce qu'on fait du reste ?[modifier | modifier le wikicode]
Les mathématiques permettent de dire s'il y a un reste ou non. Mais ce qu'on en fait dépend de la situation. Parfois, il n'y a pas de solution logique. Mais prenons un autre exemple.
Un collectionneur a 26 timbres, qu'il colle dans un petit album. Chaque page de l'album peut contenir 6 timbres. De combien de pages a-t-il besoin pour les coller tous ?
On effectue avec reste .
Quelle est la réponse ?
La division et les nombres décimaux[modifier | modifier le wikicode]
Toutes les divisions que nous avons vues parlaient de nombres entiers (1, 2, 3, 4, etc.). Mais dans certaines situations, cela ne suffit pas. Par exemple, si on partage trois bonbons entre deux personnes, on aura envie d'en donner un et demi à chacun. Les nombres décimaux permettent cela.
3:2 = 1,5
Une division qui multiplie ![modifier | modifier le wikicode]
À faire à la calculatrice, par exemple.
Plus le diviseur est petit, plus le quotient est grand. 35:7=5, 35:5=7, 35:1=35... Que se passe-t-il si on divise par un nombre plus petit que 1 ?
12:0,5=24 (sur la calculatrice, 12÷0.5=)
On vient de multiplier par 2 en utilisant la division !
Une division sans fin[modifier | modifier le wikicode]
Même en utilisant les nombres décimaux, certaines divisions n'ont jamais de fin. Par exemple, 4:3 ne se finit jamais. Il y aura toujours un reste. La calculatrice affichera une valeur approchée (arrondie).
Poser une division[modifier | modifier le wikicode]
Il existe de nombreuses façons de poser une division, selon le pays ou les habitudes. La méthode habituelle consiste à chercher combien il y a de fois le diviseur dans le nombre à diviser (le dividende).
En France, on utilise une potence ![]() pour les calculs posés (de division).
pour les calculs posés (de division).
La technique à la française[modifier | modifier le wikicode]
Comment faire ?
Avec 9, je fais combien de paquets de 4 ?
et
Je baisse mon 7.
Avec 17 je fais combien de paquets de 4 ?
et
Je baisse mon 8.
Avec 18, je fais combien de paquets de 4 ?
et
et avec le quotient et le reste.
Voir aussi[modifier | modifier le wikicode]
|
|