Preuve par Euclide du théorème de Pythagore
|
Une maintenance de cette page a été demandée. (mars 2023) Les actions suivantes sont à faire :
|
La première preuve écrite retrouvée du théorème de Pythagore se trouve dans les Éléments d'Euclide. Euclide était un mathématicien grec du IIIe siècle av. J-C, qui a vécu et travaillé à Alexandrie. Ce livre n'est connu que par ses traductions ; il résume une partie des connaissances en géométrie développés par la civilisation grecque.
Le théorème de Pythagore affirme : « Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des petites longueurs. »
Ce résultat est énoncé dans la proposition 47 du livre 1 des Éléments.
Préparation[modifier | modifier le wikicode]
La preuve d'Euclide s'appuie sur des calculs d'aire. Dans la figure à droite, on a représenté un triangle ABC rectangle en A. Le théorème de Pythagore affirme :
Dans cette relation, a2, b2 et c2 sont les aires des carrés représentés sur la figure. Par conséquent, l'aire du carré rouge est la somme des carrés bleu et vert : c'est ce que dit le théorème de Pythagore. Et c'est ce qu'Euclide va démontrer.
Il existe aujourd'hui de nombreuses preuves. Certaines consistent à diviser le carré rouge en pièces élémentaires (triangles, petits carrés, trapèzes, ...), puis à les déplacer et les recomposer en deux carrés distincts. Ce n'est pas exactement ce que fait Euclide. Les transformations, comme les translations, sont ignorées dans son traité. Pour les philosophes grecs, la géométrie est essentiellement statique et concerne la sphère céleste. Les déplacements appartiennent à la physique et seraient propres au monde terrestre.
Euclide démontre l'égalité de deux triangles de la manière suivante : un triangle est déterminé par un angle, et par les longueurs des deux côtés qui le touchent.
La preuve qui suit n'est pas exactement celle donnée par Euclide. On la connaît indirectement à travers des traductions qui ne sont pas fidèles.
Notations[modifier | modifier le wikicode]
Sur les côtés [AB], [AC] et [BC], on construit les carrés ABSR, CBTU, et ACPQ. La hauteur issue de A coupe les droites (BC) et (TU) en les points M et N. On obtient une division du carré UCTB en deux rectangles CMNU et TNMB. Par conséquent :
Euclide démontre les égalités :
Ces égalités impliquent le théorème de Pythagore.
L'argument d'Euclide[modifier | modifier le wikicode]
L'aire de BMNT est le double de l'aire du triangle BMT. L'aire de ABSR est le double du triangle ABS. On va donc s'intéresser à ces deux triangles représentés que la figure à droite.
Comme ABSR est un carré, l'angle géométrique (BS, BA) est un angle droit. De même, l'angle (BC, BT) est aussi un angle droit. De suite :
Par conséquent, les triangles BCS et BAT sont égaux au sens d'Euclide. Aujourd'hui, on dirait que BAT est l'image de BCS par une rotation de centre B et d'angle +90.
Les triangles ont donc même aire.
Conclusion[modifier | modifier le wikicode]
Dans la figure précédente, les triangles ABT et BCS ont un angle égal compris entre deux côtés égaux, |alt=Triangles de même base et même hauteur|vignette|376x376px| Triangles de même base et même hauteur ]] ce sont des triangles égaux. A ce titre ils ont la même aire.
Petit rappel : Aire d'un triangle : Tous les triangles ABC de la figure
ci-contre ont la même base et la même hauteur, donc ils ont la même aire.
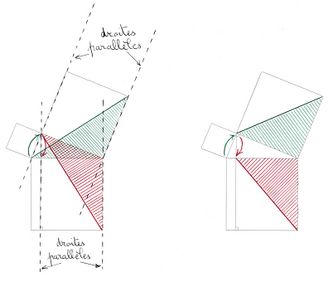
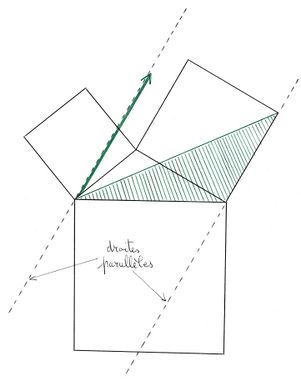
Euclide utilise cette évidence en faisant glisser le sommet d'un triangle parallèlement à son côté opposé, d'où les schémas ci-dessous.
Dans les schémas suivants les aires vertes sont égales aux aires rouges.
Le dernier schéma nous donne : c² = a² + b², c'est l'égalité du théorème de Pythagore.
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux
autres côtés.
Si le triangle de départ n'est pas rectangle, on ne peut pas faire glisser le sommet des triangles rouges et verts pour donner le même résultat. Dans ce cas le théorème de Pythagore ne s'applique pas.
|