Produit vectoriel

Le produit vectoriel de deux vecteurs est un vecteur dont les coordonnées dépendent de celles des deux vecteurs de départ (contrairement au produit scalaire où le résultat du produit de deux vecteurs est un scalaire (un nombre)). Le produit vectoriel s'applique seulement dans un espace en trois dimensions.

Le produit vectoriel entre deux vecteurs (ici ${\vec {a}}$ et ${\vec {b}}$) s'écrit de la manière suivante : ${\vec {a}}\wedge {\vec {b}}$. Le symbole ∧ entre les deux vecteurs est le symbole du produit vectoriel, qui se lit "vectoriel",

Le produit vectoriel peut être exprimé de manière géométrique ou algébrique. Ces deux approches sont bien sûr équivalentes.

La formule du produit vectoriel, par l'approche géométrique, est la suivante:

${\vec {a}}\wedge {\vec {b}}=\|{\vec {a}}\|\times \|{\vec {b}}\|\times \sin(\theta )\times {\vec {c}}$

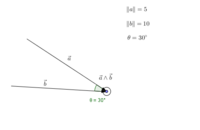
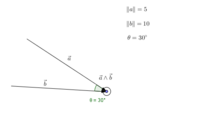
Cette formule nous dit que le produit vectoriel du vecteur a et du vecteur b est égal à la norme du vecteur a multiplié par celle du vecteur b, le tout multiplié par le sinus du plus petit angle (noté θ) formé par ces vecteurs, le tout multiplié par le vecteur c qui est un vecteur unitaire (dont la norme est égale à un) perpendiculaire aux deux autres vecteurs.

La formule du produit vectoriel, par l'approche algébrique, est la suivante:

${\vec {a}}\wedge {\vec {b}}={\begin{pmatrix}a_{x}\\a_{y}\\a_{z}\\\end{pmatrix}}\wedge {\begin{pmatrix}b_{x}\\b_{y}\\b_{z}\\\end{pmatrix}}={\begin{pmatrix}a_{y}\times b_{z}-a_{z}\times b_{y}\\-a_{x}\times b_{z}+a_{z}\times b_{x}\\a_{x}\times b_{y}-a_{y}\times b_{x}\\\end{pmatrix}}$

Calcul à partir de la norme de deux vecteurs

Un exemple de produit vectoriel

Prenons l'exemple donné par l'image on peut donc déterminer le produit vectoriel des vecteurs a et b.

L'exemple résolu

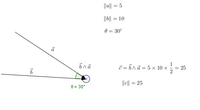
On remplace les termes de la formule: $5\times 10\times \sin(30)\times {\vec {c}}$

On multiplie 5 et 10, le sinus de 30° étant 1/2, on supprime également le vecteur n, car multiplier par 1 revient à ne rien faire, on a donc: $50\times {\frac {1}{2}}=25$ donc la norme du vecteur c est égale à 25. On note le produit vectoriel par un point dans un rond si le sens est du bas vers le haut et si le sens du vecteur est du haut vers le bas on note une croix dans un rond.

La règle dite de la main droite, on place le pouce dans le sens du vecteur a, l'index dans le sens du vecteur b et le majeur nous donne le sens de c

On a la norme du vecteur c, mais on n'a ni sa direction, ni son sens. Pour les trouver on va utiliser la règle dite de la main droite. On prend sa main droite (même si l'on est gaucher), on met le pouce dans le sens du vecteur a et l'index dans le sens du vecteur b et en tendant le majeur on obtient le sens du vecteur c.

Que se passe t'il lorsque l'on veut faire le produit vectoriel de b et de a. Seul le sens et la notation change

Lorsque l'on calcule le produit vectoriel du vecteur b et du vecteur a, le vecteur c à toujours la même norme et la même direction, mais le sens est différent.

Calcul à partir des coordonnées de deux vecteurs

On peut également calculer le produit vectoriel avec les coordonnées x, y et z de ces vecteurs dans l'espace à trois dimensions.

Nous avons la formule algébrique:

${\vec {a}}\wedge {\vec {b}}={\begin{pmatrix}a_{x}\\a_{y}\\a_{z}\\\end{pmatrix}}\wedge {\begin{pmatrix}b_{x}\\b_{y}\\b_{z}\\\end{pmatrix}}={\begin{pmatrix}a_{y}\times b_{z}-a_{z}\times b_{y}\\a_{z}\times b_{x}-a_{x}\times b_{z}\\a_{x}\times b_{y}-a_{y}\times b_{x}\\\end{pmatrix}}$

Imaginons que les coordonnées du vecteur a sont (5;-6;3) et celle du vecteur b sont (-2;7;4).Maintenant utilisons la sur nos coordonnées:

${\vec {a}}\wedge {\vec {b}}={\begin{pmatrix}5\\-6\\3\ \end{pmatrix}}\wedge {\begin{pmatrix}-2\\7\\4\\\end{pmatrix}}={\begin{pmatrix}-6\times 4-3\times 7\\3\times -2-5\times 4\\5\times 7-(-6)\times -2\\\end{pmatrix}}={\begin{pmatrix}-24-21\\-6-20\\35-12\\\end{pmatrix}}={\begin{pmatrix}-45\\-26\\23\\\end{pmatrix}}$

Donc les coordonnées du produit vectoriel sont (-45;-26;23).

Il existe également une autre méthode algébrique équivalente, mais qui fait appel à la notion de déterminant.

Différences entre un produit vectoriel et un produit scalaire

Le produit scalaire et le produit vectoriel sont deux calculs réalisés à partir deux vecteurs de même nombre de composantes. Ils ont en revanche des différences fondamentales:

Avec le produit scalaire on obtient un scalaire (c'est-à-dire un nombre) tandis qu'avec le produit vectoriel on obtient un vecteur.

Le produit scalaire peut être calculé entre des vecteurs à 2 ou 3 composantes (voire plus, même si c'est plus difficile à représenter). En revanche le vectoriel ne peut être calculé qu'avec des vecteurs à trois composantes (espace à 3 dimensions).

Pour le produit scalaire, l'ordre des vecteurs ne modifie pas le résultat: ${\vec {a}}.{\vec {b}}={\vec {b}}.{\vec {a}}$

En revanche, pour le produit vectoriel, l'ordre a une importance. La direction et la norme restent les mêmes, mais le sens change en fonction de l'ordre des vecteurs: ${\vec {a}}\wedge {\vec {b}}=-{\vec {b}}\wedge {\vec {a}}$

L'expression algébrique du calcul vectoriel permet de le vérifier assez facilement.

Portail des mathématiques —  Les nombres, la géométrie, les grands mathématiciens...