Problème du voyageur de commerce

Un exemple de résolution du problème du voyageur de commerce

Le problème du voyageur de commerce est un problème célèbre en informatique théorique, qui a de nombreuses applications dans des domaines variés. Il consiste à trouver, pour un certain nombre de villes données, la boucle la plus courte passant par toutes les villes.

Présentation[modifier | modifier le wikicode]

Graphe représentant quatre villes et les distances les séparant

L'objectif du problème est de trouver le plus court chemin passant par un certain nombre de points, qui peuvent être des villes par exemple, et revenant au point de départ. Trouver ce plus court chemin est utile dans de nombreuses situations : cela peut permettre d'économiser du carburant pour les voitures se déplaçant d'une ville à l'autre, ou de passer moins de temps dans les transports ¹. Si Philéas Fogg voulait refaire un tour du monde en passant par tous les endroits qu'il a appréciés lors de son Tour du monde en 80 jours, résoudre ce type de problème lui permettrait de voyager plus rapidement !

Pour modéliser cette situation, on va utiliser un outil mathématique qui s'appelle un graphe. Un graphe est un objet composé de sommets (les points), et d'arêtes (les traits reliant ces points entre eux), qui portent chacune un poids donné. Dans le cas de villes sur une carte géographique, ce poids pourra être une distance entre les villes, ou bien un temps de trajet. Pour modéliser le problème, on aura donc l'ensemble des sommets constitué de l'ensemble des villes, et l'ensemble des arêtes constitué des routes entre deux villes, auxquelles on associe la distance (ou le temps de trajet) entre les deux villes. À titre d'exemple, sur l'image, on voit que la ville A et la ville B sont séparées de 4 km.

Si ce problème est célèbre, c'est pour une raison particulière : malgré son apparente simplicité, on ne sait pas trouver efficacement une solution. ² On dit qu'il est NP-complet.

Histoire[modifier | modifier le wikicode]

Ce problème a été mentionné dès 1832 dans un manuel destiné aux commis voyageurs, et est étudié depuis le XIX^ème siècle par les mathématiciens et les informaticiens. Le nom de voyageur de commerce remonte aux années 1930. C'est en 1972 que le caractère NP-complet de ce problème a été mis en évidence.

Méthodes de résolution[modifier | modifier le wikicode]

Calcul de la solution pour plusieurs dizaines de villes américaines

Il existe deux grandes familles de méthodes de résolution de ce problème : les méthodes exactes, et les méthodes approchées.

Méthodes exactes[modifier | modifier le wikicode]

Les méthodes exactes sont celles qui vont systématiquement trouver le chemin le plus court. Cependant, elles ont un inconvénient : elles demandent beaucoup de calculs. Une première méthode consiste à calculer tous les chemins possibles et à ne conserver que le plus court. Si l'on prend un ensemble de quatre villes ³ et qu'on veut calculer le plus court chemin passant par toutes les villes, en partant d'une ville en particulier, on a trois possibilités pour la première ville à visiter, deux pour la deuxième et une seule pour la dernière, puisqu'on ne va passer qu'une seule fois par chaque ville pour avoir un chemin court. On a donc au total $3\times 2\times 1=6$ parcours possibles. Pour le voir autrement, on peut numéroter les villes de 1 à 4, en partant de la première ville, on a alors :

1 2 3 4 1
1 2 4 3 1
1 3 2 4 1
1 3 4 2 1
1 4 2 3 1
1 4 3 2 1

Sur l'animation, toutes les possibilités sont successivement testées, ce qui est chronophage.

Recherche du plus court parcours par force brute

On peut d'ailleurs remarquer que les parcours 1 2 3 4 1 et 1 4 3 2 1 correspondent en réalité au même trajet effectué dans les deux sens, et qu'il en est de même pour 1 2 4 3 1 et 1 3 4 2 1, et enfin pour 1 4 2 3 1 et 1 3 2 4 1. De plus, on a ici choisi arbitrairement de partir de la ville 1, mais les distances des différents parcours seraient restées les mêmes si l'on était parti d'une autre ville : les parcours 4 1 2 3 4, au départ de la ville 4 et 1 2 3 4 1, au départ de la ville 1 font la même longueur puisque les arêtes empruntées sont identiques.

Toutefois, si on peut facilement calculer pour chacun des trois parcours distincts la distance effectuée, cela devient beaucoup plus long lorsqu'on a dix villes. Cette méthode conduit en fait à ce que l'on appelle une explosion combinatoire, c'est-à-dire que le nombre de parcours va augmenter extrêmement vite lorsqu'on augmente le nombre de villes. Pour 25 villes par exemple, il y a 310224200866619719680000 parcours différents à tester, ce qui est énorme. ⁴ Sur un ordinateur personnel, le calcul de la solution prendrait environ 50000 ans ! ⁵ La méthode consistant à calculer la longueur de chaque parcours, pour conserver le parcours le plus court, généralement qualifiée de recherche en force brute , n'est donc pas adaptée. En utilisant des méthodes plus sophistiquées, faisant appel à la programmation dynamique , les informaticiens ont réussi à faire légèrement baisser la complexité algorithmique. ⁶ La résolution exacte du problème reste toutefois très coûteuse en temps de calcul. Pour pallier à ce défaut majeur, des méthodes approchées ont été élaborées.

Méthodes approchées⁷[modifier | modifier le wikicode]

D'autres méthodes moins gourmandes en temps de calcul existent pour résoudre le problème. Étant approchées, elles ne renvoient pas forcément le chemin le plus court. Toutefois, elles garantissent généralement que la solution n'est pas trop mauvaise. Parmi ces méthodes, une des plus connues est celle utilisant des algorithmes gloutons. Un algorithme glouton est un algorithme qui, à chaque fois qu'il doit effectuer un choix (entre deux routes, entre plusieurs parts de gâteau , etc.), choisit la solution la plus avantageuse pour lui à ce moment précis. On dit qu'il fait à chaque étape un choix localement optimal. Dans le cas qui nous intéresse, en partant d'une ville au hasard, l'algorithme cherchera par exemple systématiquement à rejoindre la ville non visitée la plus proche. On appelle cette technique la méthode du plus proche voisin. Un algorithme de résolution du problème ressemblera alors à :

Gauche : plus court circuit - Droite : circuit trouvé par un algorithme glouton

  Fonction glouton (n = nombre de villes)
     ville_actuelle := A
     liste_villes_visitees := [ville_actuelle]
     liste_villes_non_visitees := [B, C, D, E, ..., n - 1]
     Pour i de 2 jusqu'à n avec un pas de 1
           ville_plus_proche := premier élément de liste_villes_non_visitees
           distance_mini := distance(ville_actuelle, ville_plus_proche)
           Pour ville dans liste_villes_non_visitees
               Si distance(ville_actuelle, ville) est plus petite que distance_mini alors
                   distance_mini := distance(ville_actuelle, ville)
                   ville_plus_proche := ville
           fin Pour
           Ajouter ville_plus_proche à liste_villes_visitees
           Enlever ville_plus_proche de liste_villes_non_visitees
    fin Pour
    Renvoyer liste_villes_visitees
  Fin Fonction

Autrement dit, cet algorithme glouton part d'une ville et va à chaque fois choisir la ville la plus proche pour son prochain trajet.

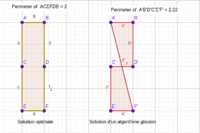
Cependant, une somme de solutions optimales localement n'est pas toujours une solution globalement optimale, comme on le voit sur l'image. Toutefois, les algorithmes gloutons restent pertinents pour calculer des solutions approchées peu coûteuses en temps de calcul. Pour une répartition aléatoire de villes, il a ainsi été calculé que les solutions qu'ils donnent sont en moyenne 25 % plus longues que les solutions exactes ⁸, ce qui est plutôt correct.

Exemple d'algorithme de recuit simulé : pour trouver la température la plus élevée, le programme va être amené à passer par des solutions moins bonnes de temps à autres

Deux autres techniques sont l'utilisation des algorithmes génétiques ou de la méthode du recuit simulé pour trouver une solution approchée.

Pour en savoir plus, lis l’article : algorithme génétique.

Le recuit simulé, par analogie avec la métallurgie, permet d'éviter que l'algorithme soit bloqué sur une solution qui soit un minimum (ou maximum selon ce que l'on cherche) local. Par exemple, si l'on veut trouver la température la plus élevée, comme sur l'animation ci-contre, il faut accepter d'avoir de temps en temps une solution moins bonne pour éviter de se retrouver bloqué dans des maxima locaux .

		Le savais-tu ?
	Des voyageuses inspirantes : les fourmis
Une autre approche récente pour résoudre le problème se base sur des algorithmes inspirés du comportement des fourmis. En effet, lorsqu'elles se déplacent entre leur fourmilière et une source de nourriture, les fourmis vont collectivement réussir à trouver le chemin le plus court. Cela est dû au fait qu'une fourmi laisse des phéromones sur le chemin qu'elle a suivi. Plus le chemin suivi est court, plus la fourmi va pouvoir l'imprégner de phéromones en repassant dessus fréquemment, ce qui va inciter ses congénères à emprunter également cette route. Cette idée peut être adaptée au voyageur de commerce

Exemple de résolution à l'aide d'un algorithme colonie de fourmis : * 1 : une fourmi effectue un parcours au hasard et trace une piste de phéromones * 2 : l'ensemble des fourmis effectue des parcours ; plus le trajet est rapide, plus les fourmis y passent et laissent donc des phéromones * 3 : chaque arête du meilleur chemin comporte donc plus de phéromones que les autres * 4 : on a trouvé le plus court chemin !

Exemples d'application du problème du voyageur de commerce[modifier | modifier le wikicode]

Le problème du voyageur de commerce a de nombreuses applications. Tout d'abord, il est bien sûr utile pour optimiser les déplacements, mais pas seulement ceux des commis voyageurs. Par exemple, connaître le plus court chemin passant par un certain nombre d'endroits permet d'organiser les itinéraires des bus scolaires. En rajoutant quelques contraintes, on peut représenter une situation où un certain nombre d'infirmiers doivent passer visiter des malades, en minimisant le temps de trajet. ⁹ D'un point de vue pédagogique, il est fréquemment utilisé en cours d'informatique pour introduire le concept de complexité algorithmique.

Ce problème est également utilisé dans des situations plus surprenantes : il est ainsi utile pour le séquençage du génome, et est aussi utilisé dans l'industrie des microprocesseurs pour la fabrication des circuits imprimés. Enfin, il sert à optimiser le déplacement des grands télescopes, car les mouvements effectués sont très lents et doivent donc être limités pour laisser du temps à l'observation du ciel.

		Le savais-tu ?
	Le Père Noël et le problème du voyageur de commerce
Étant en capacité de visiter toutes les maisons de tous les enfants du monde en l'espace de 24h, le Père Noël doit probablement disposer d'un algorithme perfectionné pour calculer son itinéraire. En effet, rien qu'en France, il doit visiter 29 millions de foyers en moins d'une nuit. Connaître un parcours optimal a donc une importance cruciale afin qu'il puisse distribuer tous ses cadeaux la nuit de Noël !

Voir aussi[modifier | modifier le wikicode]

Notes et références[modifier | modifier le wikicode]

↑ Ce qui laisse plus de temps pour faire autre chose, comme contribuer sur Vikidia !
↑ 'Efficace' veut ici dire que le temps d'exécution n'augmente pas exponentiellement en fonction de la taille des données d'entrée, le nombre de villes par exemple.
↑ N'hésite pas à prendre une feuille et un crayon pour tester par toi-même !
↑ Plus précisément, pour $n$ villes, il y a ${\frac {(n-1)!}{2}}$ parcours différents, où le ! indique une factorielle, c'est-à-dire ici le produit $(n-1)\times (n-2)\times (n-3)\times \ldots \times 3\times 2\times 1$

↑ En supposant que calculer la longueur d'un parcours demande une seule opération à l'ordinateur, on peut calculer ce temps de calcul avec un petit programme Python comme

def factorielle(n):
    if n == 1:
        return 1
    return n * factorielle(n-1)

n = 25   # nombre de villes
nb_operations = factorielle(n - 1) // 2 # nombre total de parcours à traiter

temps_secondes = nb_operations / 200e9 #200GFLOPS, une vitesse de calcul plausible pour un très bon ordinateur personnel en 2013 d'après WP

print("Il faut {} secondes pour effectuer ce calcul".format(temps_secondes))
print(round(temps_secondes / (3600 * 24), 2), "jours") 
print(round(temps_secondes / (3600 * 24 * 365.25), 2), "ans")

↑ Les meilleurs algorithmes exacts ont une complexité en ${\mathcal {O}}(n^{2}e^{n})$ , ce qui veut dire que pour $n$ villes, le nombre d'opérations à effectuer sera d'environ $n\times n\times e^{n}$ , avec $e$ la fonction exponentielle
↑ En jargon informatique, on appelle aussi ces méthodes des heuristiques
↑ Partie Heuristiques sur l'article 'Travelling salesman problem' de Wikipedia
↑ Thèse illustrant l'utilisation du problème du voyageur de commerce dans le milieu médical

Sources et liens externes[modifier | modifier le wikicode]

Article d'Interstices sur le Problème du voyageur de commerce, avec jeu interactif
Problème du voyageur de commerce sur Wikipédia
(en) Travelling salesman problem sur Wikipedia
Mémoire sur le problème du voyageur de commerce
Cours d'informatique sur la résolution approchée en Python du problème du voyageur de commerce
Article d'Interstices sur le recuit simulé
(en) The Traveling Salesman Problem: A computational study D. Applegate, R. Bixby, V. Chvátal, W. Cook, 2006, Princeton University Press
Numérique et Sciences Informatiques - Première, p. 322, S. Bays, 2019, éditions Ellipses

[1] Ce qui laisse plus de temps pour faire autre chose, comme contribuer sur Vikidia !

[2] 'Efficace' veut ici dire que le temps d'exécution n'augmente pas exponentiellement en fonction de la taille des données d'entrée, le nombre de villes par exemple.

[3] N'hésite pas à prendre une feuille et un crayon pour tester par toi-même !

[4] Plus précisément, pour $n$ villes, il y a ${\frac {(n-1)!}{2}}$ parcours différents, où le ! indique une factorielle, c'est-à-dire ici le produit $(n-1)\times (n-2)\times (n-3)\times \ldots \times 3\times 2\times 1$

[5] En supposant que calculer la longueur d'un parcours demande une seule opération à l'ordinateur, on peut calculer ce temps de calcul avec un petit programme Python comme
def factorielle(n): if n == 1: return 1 return n * factorielle(n-1) n = 25 # nombre de villes nb_operations = factorielle(n - 1) // 2 # nombre total de parcours à traiter temps_secondes = nb_operations / 200e9 #200GFLOPS, une vitesse de calcul plausible pour un très bon ordinateur personnel en 2013 d'après WP print("Il faut {} secondes pour effectuer ce calcul".format(temps_secondes)) print(round(temps_secondes / (3600 * 24), 2), "jours") print(round(temps_secondes / (3600 * 24 * 365.25), 2), "ans")

[6] Les meilleurs algorithmes exacts ont une complexité en ${\mathcal {O}}(n^{2}e^{n})$ , ce qui veut dire que pour $n$ villes, le nombre d'opérations à effectuer sera d'environ $n\times n\times e^{n}$ , avec $e$ la fonction exponentielle

[7] En jargon informatique, on appelle aussi ces méthodes des heuristiques

[8] Partie Heuristiques sur l'article 'Travelling salesman problem' de Wikipedia

[9] Thèse illustrant l'utilisation du problème du voyageur de commerce dans le milieu médical

1

2

3

4

5

6

7

8

9

Problème du voyageur de commerce

Sommaire

Présentation[modifier | modifier le wikicode]

Histoire[modifier | modifier le wikicode]

Méthodes de résolution[modifier | modifier le wikicode]

Méthodes exactes[modifier | modifier le wikicode]

Méthodes approchées⁷[modifier | modifier le wikicode]

Exemples d'application du problème du voyageur de commerce[modifier | modifier le wikicode]

Voir aussi[modifier | modifier le wikicode]

Notes et références[modifier | modifier le wikicode]

Sources et liens externes[modifier | modifier le wikicode]

Menu de navigation

Problème du voyageur de commerce

Présentation[modifier | modifier le wikicode]

Histoire[modifier | modifier le wikicode]

Méthodes de résolution[modifier | modifier le wikicode]

Méthodes exactes[modifier | modifier le wikicode]

Méthodes approchées7[modifier | modifier le wikicode]

Exemples d'application du problème du voyageur de commerce[modifier | modifier le wikicode]

Voir aussi[modifier | modifier le wikicode]

Notes et références[modifier | modifier le wikicode]

Sources et liens externes[modifier | modifier le wikicode]

Menu de navigation

Chercher

Méthodes approchées⁷[modifier | modifier le wikicode]