Combinaison linéaire
En mathématiques, une combinaison linéaire d’objets (souvent des vecteurs1) est la somme de ces objets, chacun multiplié par un nombre.
Introduction[modifier | modifier le wikicode]
Lorsque l’on parle de vecteurs, cela implique que l’on se trouve sur une structure mathématique appelée espace vectoriel. Si l’on ne connait pas, on peut imaginer cette structure comme une planète dans l’espace : par exemple, nous connaissons bien la « planète des calculs avec des nombres » (nous nous en servons tous les jours à l’école, au magasin, …) ; cette planète a ses habitants (les nombres) et ses règles que l’on connait bien et qui s’appellent des lois de composition : l’addition et la multiplication. Ainsi, l’addition de deux habitants-nombres a pour résultat un autre habitant-nombre, et pas un autre objet mathématique qui vivrait en dehors de la planète (comme une fonction ou un vecteur) ; ce sont comme de vraies lois qui interdisent aux habitants-nombres de se comporter trop bizarrement, pour nous permettre de calculer facilement.
L’espace vectoriel est une planète un peu différente : elle est peuplée par des vecteurs et possède la même loi d’addition que la « planète des nombres », mais aussi une loi plus étrange… Cette loi dit que l’on peut multiplier les vecteurs avec des habitants d’une autre planète : la planète des nombres ! Comme cette loi « sort » de la planète-espace vectoriel, on l’appelle « loi externe ». Le résultat de la multiplication d’un habitant-vecteur par un extraterrestre-nombre est un habitant-vecteur. (Dans la pratique, la multiplication du vecteur par le nombre 3 est égale au vecteur , trois fois plus « long » que le vecteur .)
Dans une combinaison linéaire, on multiplie aussi des vecteurs par des nombres : c’est cette loi externe qui entre alors en jeu. Après avoir multiplié tous les n vecteurs voulus par des nombres, on obtient donc n nouveaux vecteurs. Ensuite, on additionne : nous avons parce que, dans un espace vectoriel, la loi « + » n’est pas externe mais interne. Le résultat de l’addition de nos n nouveaux vecteurs est donc un habitant de la même planète-espace vectoriel, c’est-à-dire un vecteur !
Conclusion : effectuer une combinaison linéaire, c’est donc « allonger » ou « rétrécir » quelques vecteurs en les multipliant par des nombres, puis tous les additionner pour faire un nouveau vecteur.
Présentation mathématique[modifier | modifier le wikicode]
Si , , … , sont n vecteurs d’un espace vectoriel E sur lequel la loi externe est notée « × », et si , , … , sont n nombres, alors :
est la combinaison linéaire de ces n vecteurs par ces n nombres. Le résultat est un vecteur de E. On peut l’écrire de façon plus courte sous la forme :
qui veut dire la même chose.
À quoi ressemble le résultat ?[modifier | modifier le wikicode]
Si l’on se représente les vecteurs comme des « flèches » dans le plan ou l’espace, nous avons parce que multiplier un vecteur par un nombre avec la loi externe de l’espace vectoriel revient à multiplier la « longueur » de ce vecteur par ce nombre ; c’est-à-dire à l’« étirer » (si le nombre est plus grand que 1), à le « rétrécir » (si le nombre est compris entre -1 et 1) ou à « inverser son sens » (si le nombre est négatif).
Mais après avoir transformé chacun des vecteurs de cette manière, qu’arrive-t-il quand on les additionne entre eux ?
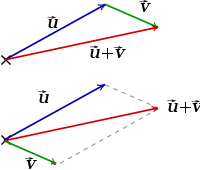
Additionner deux vecteurs entre eux, c’est créer un troisième vecteur qui parcourt à la fois le « chemin » du premier vecteur et celui du second, comme sur l’image ci-contre où l’on additionne les vecteurs et . Avec plus de deux vecteurs, c’est la même chose ! On peut donc voir le résultat d’une combinaison linéaire comme un vecteur qui pointe « au milieu » de tous les autres.
Notes et références[modifier | modifier le wikicode]
|