Utilisateur:Thilp/Brouillons/Bloc opératoire

La fonction dérivée d’une fonction est un objet des mathématiques.

C’est elle-même une fonction, qui est liée à une autre fonction par une opération appelée dérivation.

Appelons f une fonction. Sous certaines conditions, on peut la dériver pour obtenir sa fonction dérivée (ou simplement « sa dérivée »), que l’on appelle, en général, f’.

Principe

Condition d'existence de la dérivée

Article à lire : Nombre dérivé.

Appelons f une fonction et x un point où elle est définie : f transforme x en une valeur y. On écrit donc :

$f(x)=y$.

Si f admet un nombre dérivé en x, alors on dit que « f est dérivable en x ».

• Rappel : le nombre dérivé de f en un point x est le coefficient directeur  de la droite tangente à f au point x.

Quand f est dérivable sur un intervalle J (c'est-à-dire « sur plusieurs points (comme x) qui se touchent », dont on appelle le tout « J »), f admet sur cet intervalle J toute une suite de nombres dérivés. On peut alors définir f’ la fonction dérivée de f : f’ est la fonction qui associe, à tout point x de J, le nombre dérivé de f en x.

f’ permet notamment d’étudier les variations (les augmentations et les baisses) de f.

Exemple

La fonction distance D

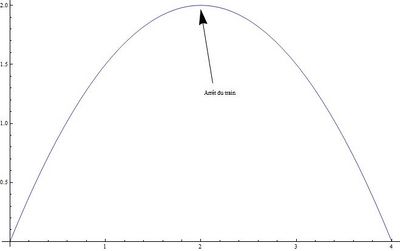
On peut inventer une fonction D (comme « distance ») qui mesure la distance entre un train et une gare. Par exemple, D(2) = 3,4 signifierait que le train se trouve à 3,4 kilomètres de notre gare, deux minutes après l'avoir quittée.

La fonction D augmente quand le train s’éloigne de la gare, puis diminue lorsqu’il y revient. La flèche indique le moment où le train s’arrête et fait demi-tour.

Si le train quitte la gare, D(t) va augmenter tant que t (le temps) augmente ; mais si le train s’arrête et revient à son point de départ, il va se rapprocher de la gare, et donc D(t) va diminuer, jusqu’à atteindre la valeur zéro quand le train est revenu dans la gare (il y a zéro kilomètres entre la gare et lui).

• L’image de droite représente la forme de la fonction D quand le train quitte la gare puis y retourne.

Dériver la fonction D permet de savoir quand elle augmente et diminue, très précisément et sans tracer son graphe. Ainsi, on voit bien, sur l’image précédente, que la fonction D « augmente » jusqu’à l’abscisse 2, puis qu’elle « diminue ». Mais la fonction dérivée de D, que l’on peut appeler D’, fournit un moyen plus pratique et plus précis pour savoir cela.

De plus, en mathématiques, dire « on voit sur le graphe de D que le train fait demi-tour en t = 2 minutes » n’est pas acceptable : en effet, le sommet de D ne se trouve peut-être pas en t = 2, mais en t = 1,9 et « 2 » n’est donc pas le bon résultat ! La méthode « visuelle » ne permet pas d’être sûr des valeurs prises par D. En revanche, la méthode « par le calcul » (c’est-à-dire par la dérivée) donne toujours le résultat exact, même lorsqu’il s’agit de nombres compliqués comme pi ou e.

La fonction D tracée plus haut admet pour dérivée la fonction D’ qui s’exprime ainsi :

$D':t\mapsto 2-t$

(on verra plus loin comment savoir que D’ vaut cela).

La dérivée de D

La fonction D (en bleu) et sa dérivée D’ (en tirets rouges). On voit que D’ coupe l’axe des abscisses (l’axe noir horizontal) quand D commence à « redescendre ».

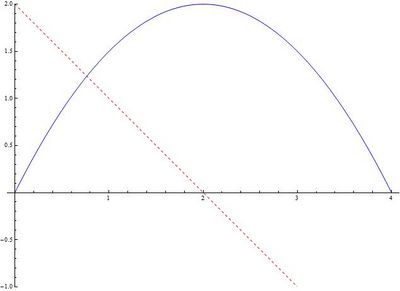
Si l’on trace maintenant le graphe des fonctions D et D’, on peut constater une chose intéressante :

• le moment où D rediminue (et où le train fait demi-tour) est exactement celui où D’ passe des valeurs positives (au dessus de l’axe horizontal noir des abscisses) aux valeurs négatives (sous cet axe).

Cela veut dire que D augmente quand D’ est positive, et que D diminue quand D’ est négative.

On peut donc facilement calculer le moment où le train fait demi-tour !

1. Ce moment correspond au « sommet » de D (puisque le train n’ira jamais plus loin que là où il fait demi-tour).
2. Ce sommet, c’est l’endroit où D n’augmente ni ne diminue.
3. C’est donc l’endroit où D’ n’est ni positive, ni négative… donc nulle.
4. Le sommet de D est donc atteint quand D’ est nulle.
5. Finalement, D’ est nulle au moment t_S tel que :

$D'(t_{S})=0$,

c’est-à-dire, puisque l’on connaît la fonction D’ :

$2-t_{S}=0$,

soit :

$t_{S}=2$.

Donc D’ est nulle au moment t_S = 2 minutes, donc le sommet de D est atteint en t_S = 2 !

On retrouve bien le résultat que l'on avait « vu » sur le graphe ; mais, cette fois-ci, on est sûr d'avoir la bonne valeur : le train fait demi-tour deux minutes après avoir quitté la gare.

Ancien article

Elle est notamment utilisée pour calculer des vitesses. En effet, pour un point qui se déplace sur une droite (que l'on peut représenter par une fonction f dépendant du temps et donnant la position sur la droite), la dérivée f' permet de connaître la vitesse de déplacement du point en fonction du temps.

Si l'on calcule la dérivée de la fonction dérivée, on obtient ce que l'on appelle la dérivée seconde. Elle correspond à l'augmentation ou à la baisse de la première dérivée. L'augmentation ou la baisse de la vitesse est l'accélération. On se sert donc généralement de la dérivée seconde pour calculer l'accélération.

Explication mathématique

Soit f une fonction.

Sa dérivée est notée f '. Le résultat de f '(x) varie selon celui de f(x), c'est-à-dire que deux fonctions différentes n'auront pas la même fonction dérivée.

Si f(x) = k où k est une constante (exemples : 2, 5, ...) alors f '(x) = 0.

Si f(x) = x alors f '(x) = 1

Si f(x)=xⁿ alors f '(x) = n × x^n-1 (exemple : si f(x) = x², alors f '(x) = 2x^2-1 = 2x¹ = 2x

Si f(x) = √x alors f'(x) = 1/2√x

Références