Problème des sept ponts de Königsberg
Le problème des sept ponts de Königsberg est un problème mathématique historique résolu par Leonhard Euler grâce à sa théorie des graphes.
Données géographiques[modifier | modifier le wikicode]
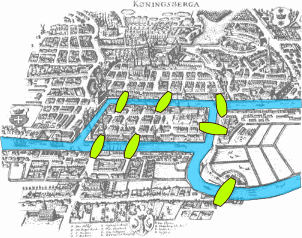
La rivière Pregel a deux affluents qui s’écoulent autour du centre de la ville de Königsberg, en Prusse orientale. Sept ponts relient les diverses rives, dont deux îles.
Euler et les sept ponts de Königsberg[modifier | modifier le wikicode]
Le problème mathématique historique[modifier | modifier le wikicode]
- Étant donné que la ville est construite sur deux îles reliées par sept ponts, trouver un chemin quelconque permettant, à partir d'un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ (étant donné qu'on ne peut traverser l'eau qu'en passant par les ponts !).
Sa résolution fut recherchée par ses habitants tout au long du XVIIIe siècle.
Léonhard Euler a montré que le problème des sept ponts de Königsberg n'a pas de solution, en appliquant une méthode de son invention, jetant ainsi les bases de la théorie des graphes.
Démonstration[modifier | modifier le wikicode]
Les deux contraintes importantes sont :
- Le promeneur doit revenir à son quartier de départ à la fin de son parcours, c’est-à-dire suivre ce qu’on appelle un cycle.
- Chaque pont doit être traversé une fois exactement (on appelle aujourd’hui « cycle eulérien » un tel cycle).
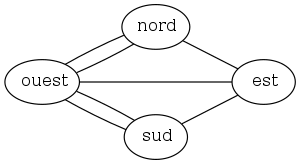
Euler a remarqué ceci :
- chaque pont ne doit être parcouru qu’une fois donc il faut autant de ponts pour quitter un quartier que pour y revenir (sinon l’on ne reviendrait jamais au point de départ) ;
- il faut donc que chaque quartier comporte un nombre pair de ponts.
Or, dans la ville de Königsberg, tous les quartiers sont reliés aux autres par un nombre impair de ponts. Par conséquent, il n’existe pas de cycle eulérien possible dans cette ville, et le problème de la promenade par les sept ponts n’a pas de solution !
|